Soal Program Linear – Ini memang kami sampikan buat anda semua sebab di situs kunci jawaban akan memberikan pembahasan lengkap bukan hanya materi Soal Program Linear ini saja tetapi berbagai dari soal Umum, Soal Sekolah Dasar, Soal MI, Soal SMP, Soal MTs, Soal SMA MA, Soal Sekolah Menengah kejuruan, Hingga Perguruan Tinggi. Tentunya dengan hal ini situs ini akan menunjukkan kelengkapan untuk anda bisa belajari pribadi untuk bahan teladan Soal tersebut.
Untuk Postingan kali ini kami bagikan secara pribadi perihal pembahasan Soal Program Linear sehingga dengan Soal Program Linear ini maka anda bisa eksklusif pelajari soal soal tersebut. Oya untuk situs kunci jawaban juga menunjukkan Bank Soal yang ada di positingan ini dimana semua postingan dan materi soal yang kami update saban hari mampu dilihat di artikel Bank Soal yang suda ada di sidebar dan header dari situ ini.
Anda bisa menyaksikan semua soal-soal tersebut lengkap tinggal pilih bahan soal yang anda ingin pelajari. Karena untuk Bank Soal tersebut adalah mencakum semua isi konten di situs kunci balasan.
Tidak usa lama-usang maka peroleh Soal Program Linear yang kami posting dibawah ini supaya bisa bermainfaat buat anda semua yang ketika ini ingin memelajari Soal Program Linear ini.
Soal Program Linear
1. Seorang pembuat kudapan manis memiliki 8.000 gr tepung dan 2.000 gr gula pasir. Ia ingin membuat dua macam kue yakni kue dadar dan kue apem. Untuk membuat kue dadar diharapkan 10 gram gula pasir dan 20 gram tepung sedangkan untuk membuat sebuah kue apem dibutuhkan 5 gram gula pasir dan 50 gram tepung. Jika kudapan manis dadar dijual dengan harga Rp 300,00/buah dan kudapan manis apem dijual dengan harga Rp 500,00/buah, tentukanlah pendapatan maksimum yang mampu diperoleh pembuat kue tersebut.
Pembahasan :
Untuk mengenali pemasukan maksimum, maka terlebih dahulu kita menyusun sistem pertidaksamaan dan fungsi tujuan dari soal cerita tersebut. Karena yang ditanya pemasukan maksimum, maka pasti harga jual kudapan manis ialah fungsi tujuan pada soal ini. Untuk menyusun sistem pertidaksamaan, yang perlu kita kerjakan adalah menentukan variabel dan koefisiennya.
Bahan yang tersedia:
Tepung = 8 kg = 8000 g
Gula = 2 kg = 2000 g
Misalkan :
Jumlah kudapan manis dadar = x
Jumlah kudapan manis apem = y
Maka jumlah tepung, gula, dan harga jual ialah koefisien. Agar lebih mudah, kita dapat memasukkan data yang ada pada soal ke dalam bentuk tabel mirip berikut :
Dari tabel di atas mampu disusun metode pertidaksamaan selaku berikut :
20x + 50y = 800 —> 2x + 5y ≤ 800
10x +5y = 2000 —> 2x + y ≤ 400
x ≥ 0 dan y ≥ 0
dengan fungsi tujuan f(x,y) = 300x + 500y
Kemudian gambarkan sistem pertidaksamaan yang telah disusun dalam grafik.
Untuk garis 2x + 5y = 800
x = 0, y = 160 —> (0, 160)
y = 0, x = 400 —> (400, 0)
Untuk garis 2x + y = 400
x = 0, y = 400 —> (0, 400)
y = 0, x = 200 —> (200, 0)
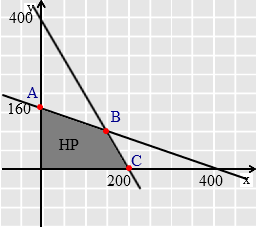
Sistem pertidaksamaan linear
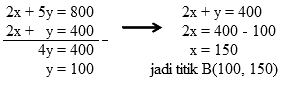
Titik B merupakan titik potong garis 2x + 5y = 800 dengan garis 2x + y = 400
Selanjutnya substitusikan titik A, B, dan C ke fungsi tujuan :
A(0, 160) —> F(x,y) = 300(0) + 500(160) = 80.000
B(100, 150) —> F(x,y) = 300(100) + 500(150) = 105.000
C(200, 0) —> F(x,y) = 300(200) + 500(0) = 60.000
Kaprikornus, pendapatan maksimum yang mampu diperoleh pedagang kudapan manis itu yakni Rp 105.000,00.
2. Menjelang hari raya Idul Adha, Pak Mahmud hendak menjual sapi dan kerbau. Harga seekor sapi dan kerbau di Medan berturut-turut Rp 9.000.000,00 dan Rp 8.000.000,00. Modal yang dimiliki pak Mahmud adalah Rp 124.000.000,00. Pak Mahmud memasarkan sapi dan kerbau di Aceh dengan harga berturut-turut Rp 10.300.000,00 dan Rp 9.200.000,00. Kandang yang ia miliki hanya dapat memuat tidak lebih dari 15 ekor. Agar mencapai keuntungan maksimum, tentukanlah banyak sapi dan kerbau yang mesti dibeli pak Mahmud.
Pembahasan :
Karena ditanya keuntungan, pasti fungsi tujuannya yakni besar laba dari pemasaran sapi dan kerbau. Untuk itu, pastikan terlebih dulu keuntungan menjual sapi dan kerbau sebagai berikut :
untung sapi = Rp 10.300.000,00 – Rp 9.000.000,00 = Rp 1.300.000,00
untung kerbau = Rp 9.200.000,00 – Rp 8.000.000,00 = Rp 1.200.000,00
Misalkan banyak sapi = x dan banyak kerbau = y, maka fungsi tujuan menjadi :
F(x,y) = 1.300.000x + 1.200.000y
Model matematika yang menyanggupi soal yaitu :
x ≥ 0 —> banyak sapi tidak mungkin negatif
y ≥ 0 —> banyak kerbau tidak mungkin negatif
x + y ≤ 15 —> alasannya adalah kandang hanya dapat menampung 15 ekor.
Karena modal Pak Mahmud Rp 124.000.000,00 maka :
9.000.000x + 8.000.000y ≤ 124.000.000 —> disederhanakan menjadi : 9x + 8y ≤ 124
Selanjutnya, kita pastikan titik koordinat masing-masing garis supaya mampu kita gambar dalam grafik.
Untuk x + y = 15
jika x = 0, maka y = 15 —> (0,15)
jika y = 0, maka x = 15 —> (15,0)
Untuk 9x + 8y = 124
jika x = 0, maka y = 15,5 —> (0, 16) —> digenapkan sebab jumlah sapi tidak mungkin 1/2.
jika y = 0, maka x = 13,7 —> (13 ,0) —> digenapkan menjadi 13 alasannya adalah menyaksikan kondisi grafik, titik ini akan menjadi titik pojok, jadi 13,7 tidak digenapkan ke 14 alasannya kalau dibulatkan ke 14 maka akan lebih dari Rp 124.000.000,00.
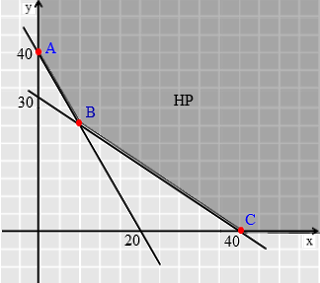
Dari grafik di atas diperoleh tiga titik pojok yang menyanggupi syarat untuk menghasilkan nilai maksimum yakni titik A, B, dan C. Titi A dan C dapat ditentukan secara langsung adalah A(0,15) dan C(13,0). Titik B ialah titik potong antara garis x + y = 15 dan 9x + 8y = 124.
x + y = 15 , maka x = 15 – y —> substitusi ke persamaan 9x + 8y = 124
9(15 – y) + 8y = 124
135 – 9y + 8y = 124
y = 11
x + y = 15
x + 11 = 15
x = 4 —-> jadi titik B(4,11)
Selanjutnya substitusi masing-masing titik ke fungsi tujuan :
A(0,15) —> f(x,y) = 1.300.000(0) + 1.200.000(15) = 18.000.000
B(4,11) —> f(x,y) = 1.300.000(4) + 1.200.000(11) = 18.400.000
C(13,0) —> f(x,y) = 1.300.000(13) + 1.200.000(0) = 16.900.000
Jadi, semoga keuntungannya maksimum, jumlah sapi dan kerbau yang harus dibeli pak Mahmud adalah 4 ekor sapi dan 11 ekor kerbau.
3. Seorang penjualmenjual buah mangga dan pisang dengan memakai gerobak. Pedagang tersebut berbelanja mangga dengan harga Rp 8.000,00/kg dan pisang Rp 6.000,00/kg. Modal yang tersedia Rp 1.200.000,00 dan gerobaknya hanya mampu menampung mangga dan pisang sebanyak 180 kg. Jika harga jual mangga Rp 9.200,00/kg dan pisang Rp 7.000,00/kg, maka tentukanlah laba maksimum yang diperoleh penjualtersebut.
Pembahasan :
Karena ditanya keuntungan maksimum, maka fungsi tujuannya yaitu laba dari memasarkan buah mangga dan buah pisang perkilonya.
Berikut untung penjualan :
mangga = 9.200 – 8.000 = 1.200
pisang = 7.000 – 6000 = 1.000
misalkan :
jumlah mangga = x
jumlah pisang = y
maka fungsi tujuannya yaitu :
F(x,y) = 1.200x + 1.000y
Model matematika atau tata cara pertidaksamaan yang menyanggupi soal tersebut adalah :
x + y ≤ 180
8.000x + 6.000y ≤ 1.200.000 —> 4x + 3y ≤ 600
x ≥ 0
y ≥ 0
Titik potong masing-masing garis terhadap sumbu x dan sumbu y :
Garis x + y = 180
untuk x = 0 , y = 180 —> (0, 180)
untuk y = 0, x = 180 —> (180,0)
Garis 4x + 3y = 600
untuk x = 0, y = 200 —> (0, 200)
untuk y = 0, x = 150 —> (150, 0)
Himpunan solusi sistem pertidaksamaan yakni :
Dari grafik dimengerti ada tiga titik pojok adalah A, B, dan C. Titik C ialah perpotongan antara garis x + y = 180 dengan 4x + 3y = 600.
Substitusi titik pojok pada fungsi objektif F(x,y) 1.200x + 1.000y :
A (0, 180) —> F(x,y) =1.000(180) = 180.000
B (60, 120) —> F(x,y) = 1.200(60) + 1.000(120) = 192.000
C (150,0) —> F(x,y) = 1.200(150) = 180.000
Jadi laba maksimum yang diperoleh pedagang buah yaitu Rp 192.000,00.
4. Sebuah perusahaan properti memproduksi dua macam lemari pakaian yakni tipe lux dan tipe sport dengan menggunakan 2 materi dasar yang serupa ialah kayu jati dan cat pernis. Untuk memproduksi 1 unit tipe lux diperlukan 10 batang kayu jati dan 3 kaleng cat pernis, sedangkan untuk memproduksi 1 unit tipe sport diperlukan 6 batang kayu jati dan 1 kaleng cat pernis. Biaya produksi tipe lux dan tipe sport masing-masing yaitu Rp 40.000 dan Rp 28.000 per unit. Untuk satu abad produksi, perusahaan menggunakan paling sedikit 120 batang kayu jati dan 24 kaleng cat pernis. Bila perusahaan harus memproduksi lemari tipe lux paling sedikit 2 buah dan tipe sport paling sedikit 4 buah, tentukan banyak lemari tipe lux dan tipe sport yang harus dibuat agar ongkos produksinya minimum.
Pembahasan:
Karena yang ditanya yakni ongkos buatan minimum, maka biaya buatan masing-masing tipe lemari ialah fungsi tujuannya. Bila kita misalkan tipe lux = x dan tipe sport = y, maka fungsi tujuannya yakni sebagai berikut :
F(x,y) = 40.000x + 28.000y
Selanjutnya, versi matematika untuk hambatan yang diberikan ialah mirip di bawah ini. Perhatikan bahwa tanda pertidaksamaan yang dipakai untuk soal penentuan nilai minimum ialah lebih dari sama dengan (≥) mirip di bawah ini :
x ≥ 2 —> karena tipe lux paling sedikit 2 buah
y ≥ 4 —> alasannya tipe sport paling sedikit 4 buah
10x + 6y >= 120 —> kayu jati yang dipakai paling sedikit 120 batang
3x + y ≥ 24 —> cat pernis yang dipakai paling sedikit 24 kaleng
Titik potong masing-masing hambatan terhadap sumbu x dan sumbu y yaitu selaku berikut :
untuk 10x + 6y = 120
misal x = 0, maka y = 20 —> (0,20)
misal y = 0, maka x = 12 —> (12,0)
untuk 3x + y = 24
misal x = 0, maka y = 24 —> (0,24)
misal y = 0, maka x = 8 —> (8,0)
Setelah itu kita gambarkan grafik sesuai dengan titik-titik yang telah kita peroleh dan tentukan daerah himpunan penyelesaiannya. Karena lebih besar sama dengan (>=), maka daerah himpunan penyelesaiannya yakni daerah di atas/kanan garis.
Dari garfik di atas terang tampakbahwa terdapat tiga titik pojok yang akan diuji untuk dilihat titik manakah yang menciptakan nilai minimum.
Titik C ialah perotongan antara garis y = 4 dan 10x + 6y = 120. Dengan mensubstitusi nilai y = 4 pada persamaan 10x + 6y = 120, maka diperoleh :
10x + 6(4) = 120
10x = 96
x = 9,6 = 9 —> digenapkan 9 karena mustahil 0,6 buah.
maka titik C(9,4)
Titik B merupakan perpotongan antara garis 10x + 6y = 120 dan garis 3x + y = 24. Dengan metode substitusi diperoleh :
3x + y = 24 —> y = 24 – 3x —> substitusi ke persamaan 10x + 6y = 120
10x + 6(24 – 3x) = 120
10x + 144 – 18x = 120
-8x = -24
x = 3
Sunstitusi x = 3 ke persamaan y = 24 – 3x
y = 24 – 3(3) = 15 —> titik B(3,15)
Titik A merupakan perpotongan antara garis 3x + y = 24 dengan x = 2. Dengan mensubstitusikan nilai x pada persamaan 3x + y = 24, maka diperoleh :
3(2) + y = 24
y = 24 – 6
y = 18 —> titik A(2,18)
Langkah terakhir, substitusi masing-masing titik ke fungsi tujuan F(x,y) = 40.000x + 28.000y selaku berikut :
A(2,18) —> F(x,y) = 40.000(2) + 28.000(18) = 584.000
B(3,15) —> F(x,y) = 40.000(3) + 28.000(15) = 540.000
C(9,4) —> F(x,y) = 40.000(9) + 28.000(4) = 482.000
Jadi biar biaya produksi minimum, perusahaan seharusnya memproduksi 9 buah lemari tipe lux dan 4 buah lemari tipe sport dengan ongkos bikinan Rp 482.000,00
5. Seorang pedagang mebel ingin mengirim barang dagangannya yang terdiri atas 1.200 dingklik dan 400 meja. Untuk kebutuhan tersebut, ia akan menyewa truk dan colt. Truk mampu menampung 30 kursi lipat dan 20 meja lipat, sedangkan colt mampu menampung 40 dingklik lipat dan 10 meja lipat. Ongkos sewa suatu truk Rp 200.000,00 sedangkan biaya sewa suatu colt Rp 160.000,00. Tentukan jumlah truk dan colt yang harus disewa agar ongkos pengantaran minimum.
Pembahasan :
Agar biaya kirim minimum, maka fungsi tujuannya ialah biaya sewa. Misal truk = x dan colt = y, maka fungsi maksudnya menjadi :
F(x,y) = 200.000x + 160.000y
Model matematika yang menyanggupi soal di atas yakni selaku berikut :
30x + 40y ≥1.200 —> 3x + 4y ≥ 120
20x + 10y ≥ 400 —> 2x + y ≥ 40
x >= 0
y >= 0
Tentukan titik koordinat garis kendala yang diperoleh selaku beikut :
untuk 3x + 4y ≥ 120
misal x = 0, maka y = 30 —> (0,30)
misal y = 0, maka x = 40 —> (40,0)
untuk 2x + y ≥ 40
misal x = 0, maka y = 40 —> (0,40)
misal y = 0, maka x = 20 —> (20,0)
Gambarkan ke dalam grafik dan pastikan tempat himpunan penyelesaiannya seperti berikut :
Dari grafik di atas,diperoleh titik A(0,40), B(8,24), dan C(40,0). Untuk memastikan titik mana yang menciptakan nilai minimum, ada baiknya kita uji satu-persatu.
A(0,40) —> F(x,y) = 200.000(0) + 160.000(40) = 6.400.000
B(8,24) —> F(x,y) = 200.000(8) + 160.000(24) = 5.440.000
C(40,0) —> F(x,y) = 200.000(40) + 160.000(0) = 8.000.000
Jadi supaya biaya pengantaran minimum, penjualtersebut seharusnya menyewa 8 truk dan 24 colt.
6. Seorang petani memiliki tanah tidak kurang dari 10 hektar. Ia mempersiapkan akan menanami padi seluas 2 hektar sampai dengan 6 hektar dan menanam jagung seluas 4 hektar hingga dengan 6 hektar. Untuk menanam padi perhektarnya dibutuhkan biaya Rp 400.000,00 sedangkan untuk menanam jagung per hektarnya dibutuhkan biaya Rp 200.000,00. Agar ongkos tanam minimum, tentukan berapa banyak masing-masing padi dan jagung yang harus ditanam.
Pembahasan :
Dengan memisalkan padi = x dan jagung = y, fungsi tujuan yang menyanggupi soal di atas ialah sebagai berikut :
F(x,y) = 400.000x + 200.000y
Model matematika yang menyanggupi soal di atas yaitu :
x >= 2 —> paling sedikit 2 hektar padi
x <= 6 ---> paling banyak 6 hektar padi
y >= 4 —> paling sedikit 4 hektar jagung
y <= 6 ---> paling banyak 6 hektar padi
x + y >= 10 —> tanah tidak kurang 10 hektar
Dari grafik dimengerti titik pojok A(4,6), B(6,6), dan C(6,4). Substitusi ke fungsi tujuan F(x,y) = 400.000x + 200.000y, maka diperoleh :
A(4,6) —> F(x,y) = 400.000(4) + 200.000(6) = 2.800.000
B(6,6) —> F(x,y) = 400.000(6) + 200.000(6) = 3.600.000
C(6,4) —> F(x,y) = 400.000(6) + 200.000(4) = 3.200.000
Makara supaya biaya tanam minimum, petani semestinya menanam 4 hektar padi dan 6 hektar jagung.