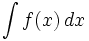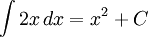Sejarah pertumbuhan kalkulus bisa ditilik pada beberapa kala zaman, yakni zaman kuno, zaman pertengahan, dan zaman terbaru. Pada kurun zaman kuno, beberapa aliran wacana kalkulus integral telah muncul, namun tidak dikembangkan dengan baik dan sistematis. Perhitungan volume dan luas yang merupakan fungsi utama dari kalkulus integral mampu ditelusuri kembali pada Papirus Moskow Mesir (c. 1800 SM) di mana orang Mesir menjumlah volume dari frustrum piramid[1]. Archimedes menyebarkan aliran ini lebih jauh dan menciptakan heuristik yang menyerupai kalkulus integral.[2]
Pada zaman pertengahan, matematikawan India, Aryabhata, memakai rancangan kecil takterhingga pada tahun 499 dan mengekspresikan masalah astronomi dalam bentuk persamaan diferensial dasar.[3] Persamaan ini lalu mengirim Bhāskara II pada kurun ke-12 untuk menyebarkan bentuk permulaan turunan yang mewakili pergantian yang sangat kecil takterhingga dan menerangkan bentuk permulaan dari “Teorema Rolle“.[4] Sekitar tahun 1000, matematikawan Irak Ibn al-Haytham (Alhazen) menjadi orang pertama yang menurunkan rumus perhitungan hasil jumlah pangkat empat, dan dengan memakai induksi matematika, ia berbagi sebuah metode untuk menurunkan rumus biasa dari hasil pangkat integral yang sungguh penting terhadap kemajuan kalkulus integral.[5] Pada masa ke-12, seorang Persia Sharaf al-Din al-Tusi mendapatkan turunan dari fungsi kubik, sebuah hasil yang penting dalam kalkulus diferensial. [6] Pada periode ke-14, Madhava, bareng dengan matematikawan-astronom dari Mazhab astronomi dan matematika Kerala, menerangkan kasus khusus dari deret Taylor[7], yang dituliskan dalam teks Yuktibhasa.[8][9][10]
Pada zaman terbaru, penemuan independen terjadi pada permulaan kurun ke-17 di Jepang oleh matematikawan seperti Seki Kowa. Di Eropa, beberapa matematikawan seperti John Wallis dan Isaac Barrow memberikan terobosan dalam kalkulus. James Gregory mengambarkan sebuah perkara khusus dari teorema dasar kalkulus pada tahun 1668.
Gottfried Wilhelm Leibniz pada mulanya dituduh memalsukan dari hasil kerja Sir Isaac Newton yang tidak dipublikasikan, tetapi kini dianggap sebagai kontributor kalkulus yang hasil kerjanya dilaksanakan secara terpisah.
Leibniz dan Newton mendorong fatwa-pemikiran ini bareng selaku sebuah kesatuan dan kedua orang ilmuwan tersebut dianggap selaku penemu kalkulus secara terpisah dalam waktu yang nyaris berbarengan. Newton mengaplikasikan kalkulus secara umum ke bidang fisika sementara Leibniz membuatkan notasi-notasi kalkulus yang banyak digunakan kini.
Ketika Newton dan Leibniz menerbitkan hasil mereka untuk pertama kali, muncul kontroversi di antara matematikawan ihwal mana yang lebih pantas untuk mendapatkan penghargaan kepada kerja mereka. Newton menurunkan hasil kerjanya terlebih dulu, namun Leibniz yang pertama kali mempublikasikannya. Newton menuduh Leibniz mencuri pemikirannya dari catatan-catatan yang tidak dipublikasikan, yang sering dipinjamkan Newton kepada beberapa anggota dari Royal Society.
Pemeriksaan secara jelas menawarkan bahwa keduanya bekerja secara terpisah, dengan Leibniz memulai dari integral dan Newton dari turunan. Sekarang, baik Newton dan Leibniz diberikan penghargaan dalam berbagi kalkulus secara terpisah. Adalah Leibniz yang menunjukkan nama kepada ilmu cabang matematika ini selaku kalkulus, sedangkan Newton menamakannya “The science of fluxions”.
Sejak itu, banyak matematikawan yang memperlihatkan bantuan kepada pengembangan lebih lanjut dari kalkulus.
Kalkulus menjadi topik yang sungguh lazim di Sekolah Menengan Atas dan universitas zaman terbaru. Matematikawan seluruh dunia terus memperlihatkan kontribusi terhadap pertumbuhan kalkulus.[11]
Pengaruh penting
Walau beberapa rancangan kalkulus telah dikembangkan terlebih dulu di Mesir, Yunani, Tiongkok, India, Iraq, Persia, dan Jepang, penggunaaan kalkulus modern dimulai di Eropa pada kurun ke-17 ketika Isaac Newton dan Gottfried Wilhelm Leibniz berbagi prinsip dasar kalkulus. Hasil kerja mereka kemudian menunjukkan efek yang besar lengan berkuasa kepada pertumbuhan fisika.
Aplikasi kalkulus diferensial mencakup perkiraan kecepatan dan percepatan, kemiringan suatu kurva, dan optimalisasi. Aplikasi dari kalkulus integral mencakup perkiraan luas, volume, panjang busur, pusat massa, kerja, dan tekanan. Aplikasi lebih jauh mencakup deret pangkat dan deret Fourier.
Kalkulus juga dipakai untuk menerima pengertian yang lebih rinci perihal ruang, waktu, dan gerak. Selama berabad-kala, para matematikawan dan filsuf berupaya memecahkan paradoks yang meliputi pembagian bilangan dengan nol ataupun jumlah dari deret takterhingga. Seorang filsuf Yunani antik memberikan beberapa pola terkenal mirip paradoks Zeno. Kalkulus memberikan penyelesaian, khususnya di bidang limit dan deret takterhingga, yang lalu berhasil memecahkan paradoks tersebut.
Prinsip-prinsip
Limit dan kecil tak terhingga
Kalkulus pada umumnya dikembangkan dengan memanipulasi sejumlah kuantitas yang sangat kecil. Objek ini, yang dapat diperlakukan selaku angka, adalah sangat kecil. Setiap perkalian dengan kecil takterhingga (infinitesimal) tetaplah kecil takterhingga, dengan kata lain kecil takterhingga tidak menyanggupi properti Archimedes. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi kecil takterhingga.
Pada kala ke-19, konsep kecil takterhingga digantikan oleh desain limit. Limit menjelaskan nilai suatu fungsi pada nilai input tertentu dengan hasil dari input terdekat. Dari sudut pandang ini, kalkulus yaitu sekumpulan teknik memanipulasi limit-limit tertentu.
Turunan
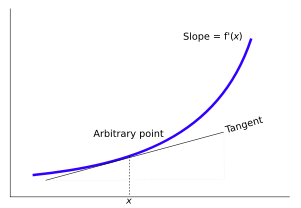
Garis singgung pada (x, f(x)). Turunan f’(x) dari sebuah kurva pada sebuah titik ialah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut.
Kalkulus diferensial adalah ilmu yang mempelajari definisi, properti, dan aplikasi dari turunan atau kemiringan dari suatu grafik.
Konsep turunan secara mendasar lebih maju dan rumit dibandingkan dengan desain yang didapatkan di aljabar. Dalam aljabar, seorang murid mempelajari sebuah fungsi dengan input sebuat angka dan output sebuah angka. Tetapi input dari turunan ialah suatu fungsi dan outputnya juga yaitu sebuah fungsi.
Untuk mengerti turunan, seorang murid harus mempelajari notasi matematika. Dalam notasi matematika, salah satu simbol yang biasanya dipakai untuk menyatakan turunan dari sebuah fungsi ialah apostrofi. Maka turunan dari f yaitu f’.
.
Jika input dari suatu fungsi yakni waktu, maka turunan dari fungsi itu adalah laju pergeseran di mana fungsi tersebut berganti.
Jika fungsi tersebut adalah fungsi linear, maka fungsi tersebut mampu ditulis dengan y=mx+b, di mana:
.
Ini menawarkan nilai dari kemiringan suatu garis lurus. Jika suatu fungsi bukanlah garis lurus, maka pergantian y dibagi kepada pergeseran x bervariasi, dan kita mampu menggunakan kalkulus untuk menentukan nilai pada titik tertentu. Kemiringan dari suatu fungsi mampu diekspresikan:
di mana koordinat dari titik pertama yakni (x, f(x)) dan h ialah jarak horizontal antara dua titik.
Untuk menentukan kemiringan dari sebuat kurva, kita memakai limit:
Sebagai pola, untuk memperoleh gradien dari fungsi f(x) = x2 pada titik (3,9):
Integral
Kalkulus integral yaitu ilmu yang mempelajari definisi, properti, dan aplikasi dari dua desain yang saling bekerjasama, integral taktentu dan integral tertentu. Proses pencarian nilai dari suatu integral dinamakan pengintegralan (integration). Dengan kata lain, kalkulus integral mempelajari dua operator linear yang saling bekerjasama.
Integral taktentu yaitu antiturunan, yakni kebalikan dari turunan. F yaitu integral taktentu dari f saat f yaitu turunan dari F.
Integral tertentu memasukkan suatu fungsi dengan outputnya ialah suatu angka, yang mana memperlihatkan luas antar grafik yang dimasukkan dengan sumbu x.
Contohnya yaitu jarak yang ditempuh dengan lama waktu tertentu
Jika kecepatannya yakni konstan, perkiraan bisa dilaksanakan dengan perkalian, namun jikalau kecepatan berubah, maka dibutuhkan sebuah sistem yang lebih canggih. Salah satu tata cara tersebut ialah memperkirakan jarak tempuh dengan memecahkan usang waktu menjadi banyak interval waktu yang singkat, lalu dikalikan dengan usang waktu tiap interval dengan salah satu kecepatan di interval tersebut, dan lalu menambahkan total keseluruhan jarak yang didapat. Konsep dasarnya yakni, kalau interval waktu sangat singkat, maka kecepatan dalam interval tersebut tidak berubah banyak. Namun, penjumlahan Riemann cuma menawarkan nilai asumsi. Kita harus mengambil suatu limit untuk mengdapatkan hasil yang tepat.
Integral mampu dianggap sebagai penelusuran luas kawasan di bawah kurva f(x), antara dua titik a dan b.
Jika f(x) pada diagram di samping mewakili kecepatan yang berubah-ubah, jarak yang ditempuh antara dua waktu a dan b ialah luas tempat S yang diarsir.
Untuk memperkirakan luas, sistem intuitif yakni dengan membagi jarak antar a dan b menjadi beberapa segmen yang serupa besar, panjang setiap segmen disimbolkan Δx. Untuk setiap segmel, kita dapat menentukan satu nilai dari fungsi f(x). Nilai tersebut misalkan yaitu h. Maka luas tempat persegi panjangan dengan lebar Δx dan tinggi h menawarkan nilai jarak yang ditempuh di segmen tersebut. Dengan menjumlahkan luas setiap segmen tersebut, maka didapatkan asumsi jarak tempuh antara a dan b. Nilai Δx yang lebih kecil akan memperlihatkan perkiraan yang lebih baik, dan menerima nilai yang sempurna dikala kita menngambil limit Δx mendekati nol.
Simbol dari integral adalah , berupa S yang dipanjangkan (kependekan dari “sum”). Integral tertentu ditulis sebagai
dan dibaca “Integral dari a ke b dari f(x) kepada x.”
Integral tak pasti, atau anti derivatif, ditulis:
.
Oleh alasannya adalah turunan dari fungsi y = x2 + C yakni y ‘ = 2x (di mana C yaitu konstanta),
.
Teorema dasar
Teorema dasar kalkulus menyatakan bahwa turunan dan integral adalah dua operasi yang saling bertentangan. Lebih tepatnya, teorema ini menghubungkan nilai dari anti derivatif dengan integral tertentu. Karena lebih mudah menghitung suatu anti derivatif daripada mengaplikasikan definisi dari integral, teorema dasar kalkulus menawarkan cara yang simpel dalam menjumlah integral tertentu.
Teorema dasar kalkulus menyatakan: Jika suatu fungsi f adalah kontiniu pada interval [a,b] dan jika F ialah fungsi yang mana turunannya adalah f pada interval (a,b), maka
Lebih lanjut, untuk setiap x di interval (a,b),
Aplikasi
Kalkulus digunakan di setiap cabang sains fisik, sains komputer, statistik, teknik, ekonomi, bisnis, kedokteran, kependudukan, dan di bidang-bidang lainnya.
Setiap konsep di mekanika klasik saling berhubungan melalui kalkulus. Massa dari sebuah benda dengan massa jenis yang tidak diketahui, momen inersia dari suatu objek, dan total energi dari suatu objek mampu diputuskan dengan memakai kalkulus. Dalam subdisiplin listrik dan magnetisme, kalkulus mampu dipakai untuk mencari total fluks dari suatu medan elektromagnetik . Contoh historik lainnya adalah penggunaan kalkulus di hukum gerak Newton, diekspresikan dengan laju pergeseran yang merujuk pada turunan: Laju pergeseran saat-saat dari sebuah benda yakni sama dengan resultan gaya yang bekerja bada benda tersebut dengan arah yang sama. Bahkan rumus biasa dari hukum ke-dua Newton: Gaya = Massa × Percepatan, mengandung diferensial kalkulus alasannya adalah percepatan mampu diekspresikan sebagai turunan dari kecepatan. Teori elektromagnetik Maxwell dan teori relativitas Einstein juga diekspresikan dengan diferensial kalkulus.
Referesi Sumber DAFTAR PUSTAKA
- ^ Helmer Aslaksen. Why Calculus? National University of Singapore. See
- ^ Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7
- ^ Aryabhata the Elder
- ^ Ian G. Pearce. Bhaskaracharya II.
- ^ Victor J. Katz (1995). “Ideas of Calculus in Islam and India”, Mathematics Magazine 68 (3), pp. 163-174.
- ^ J. L. Berggren (1990). “Innovation and Tradition in Sharaf al-Din al-Tusi’s Muadalat”, Journal of the American Oriental Society 110 (2), pp. 304-309.
- ^ Madhava. Biography of Madhava. School of Mathematics and Statistics University of St Andrews, Scotland. Diakses pada 13 September 2006
- ^ An overview of Indian mathematics. Indian Maths. School of Mathematics and Statistics University of St Andrews, Scotland. Diakses pada 7 Juli 2006
- ^ Science and technology in free India. Government of Kerala — Kerala Call, September 2004. Prof.C.G.Ramachandran Nair. Diakses pada 9 Juli 2006
- ^ Charles Whish (1835). Transactions of the Royal Asiatic Society of Great Britain and Ireland.
- ^ UNESCO-World Data on Education [isapi.dll?clientID=137079235&infobase=iwde.nfo&softpage=PL frame]
Daftar Pustaka
- Donald A. McQuarrie (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 978-1-891389-24-5
- James Stewart (2002). Calculus: Early Transcendentals, 5th ed., Brooks Cole. ISBN 978-0-534-39321-2
Buku Online
- Crowell, B., (2003). “Calculus” Light and Matter, Fullerton. Retrieved 6th May 2007 from http://www.lightandmatter.com/calc/calc.pdf
- Garrett, P., (2006). “Notes on first year calculus” University of Minnesota. Retrieved 6th May 2007 from http://www.math.umn.edu/ garrett/calculus/first_year/notes.pdf
- Faraz, H., (2006). “Understanding Calculus” Retrieved Retrieved 6th May 2007 from Understanding Calculus, URL http://www.understandingcalculus.com/ (HTML only)
- Keisler, H. J., (2000). “Elementary Calculus: An Approach Using Infinitesimals” Retrieved 6th May 2007 from http://www.math.wisc.edu/ keisler/keislercalc1.pdf
- Mauch, S. (2004). “Sean’s Applied Math Book” California Institute of Technology. Retrieved 6th May 2007 from http://www.cacr.caltech.edu/ sean/applied_math.pdf
- Sloughter, Dan., (2000) “Difference Equations to Differential Equations: An introduction to calculus“. Retrieved 6th May 2007 from http://math.furman.edu/ dcs/book/
- Stroyan, K.D., (2004). “A brief introduction to infinitesimal calculus” University of Iowa. Retrieved 6th May 2007 from http://www.math.uiowa.edu/ stroyan/InfsmlCalculus/InfsmlCalc.htm (HTML only)
Strang, G. (1991) “Calculus” Massachusetts Institute of Technology. Retrieved 6th May 2007 from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm.