Pada artikel kali ini kita akan membahas mengenai Pythagoras.
Pada bahan bangun datar tentu kalian mempelajari bahan segitiga. Terdapat beberapa jenis segitiga diantaranya segitiga lancip, segitiga tumpul, dan segitiga siku-siku.
Terdapat salah satu bahan yang berkaitan degan segitiga siku-siku ialah teorema Pythagoras. Teorema ini berkaitan dengan salah satu tokoh matematika bernama Pythagoras.
Apakah kalian mengetahui bagaimana teorema Pythagoras itu?
Untuk memahaminya, perhatikan penjelasan berikut.
Daftar Isi
Definisi Pythagoras
Pythagoras merupakan salah satu teorema atau aturan dalam matematika yang membahasa tentang keterkaitan segi-segi segitiga, dalam hal ini ialah segitiga siku-siku.
Teorema pythagoras ditemukan oleh seorang filsum Yunani bernama Pythagoras. Teorem ini ditemukan pada abad ke-6.
Perhatikan klarifikasi perihal pola penerapan pythagoras berikut.
Penerapan Pythagoras
Contoh penerapan pythagoras mampu dilihat pada bidang pertukangan. Tukang bangunan biasanya memakai penggaris siku untuk memilih bahwa sudut yang dibentuk oleh pondasi bangunan ialah sudut siku-siku.
Selain itu, tukang biasanya juga menciptakan kerangka atap yang menerapkan desain pythagoras.
Selain itu juga untuk menentukan jarak terdekat dari dua posisi mampu dengan gampang diputuskan memakai teorema pythagoras.
Selanjutnya akan dijelaskan tentang teorema pythagoras.
Teorema Pythagoras
Teorema pythagoras menyatakan bahwa kuadrat sisi miring segitiga siku-siku (hipotenusa) sama dengan jumlah kuadrat segi-segi yang saling berpenyiku.
Atau secara sederhana dapat diterangkan bahwa jika sisi terpanjang segitiga siku-siku dikuadratkan maka akan sama dengan jumlah dari kuadrat segi yang yang lain.
Selanjutnya akan diterangkan mengenai rumus pythagoras.
Rumus Pythagoras
Dari pembuktian di atas dapat dirumuskan teorema pythagoras sebagai berikut.
Misalkan terdapat segitiga siku-siku dengan ukuran segi masing-masing ialah a, b, dan c.
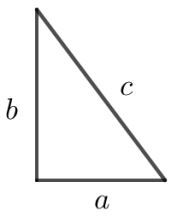
Rumus Pythagoras dari segitiga siku-siku di atas yakni a2 + b2 = c2
Keterangan:
a, b, c : ukuran segi-segi segitiga.
Bagaimana jikalau a2 + b2 < c2 atau a2 + b2 > c2?
- Jika a2 + b2 < c2 maka jenis segitiganya yakni segitiga lancip.
- Jika a2 + b2 > c2 maka jenis segitiganya ialah segitiga tumpul.
- Jika a2 + b2 = c2 maka jenis segitiganya ialah segitiga siku-siku.
Berikut akan dijelaskan salah satu pembuktian teorema pythagoras.
Pembuktian Teorema Pythagoras
Terdapat banyak tata cara/cara dalam pembuktian teorema pythagoras. Pembuktian ini disebut selaku pembuktian Bhaskara diambil dari nama penemunya yaitu Bhaskara dari India.
Perhatikan gambar berikut.
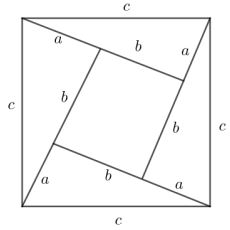
Pada gambar tersebut terdapat persegi dengan segi berskala c dan persegi kecil dengan ukuran (b – a), serta empat buah segitiga siku-siku dengan ukuran sisi a, b, dan c. Pembuktian teorema pythagorasn yakni selaku berikut.
Luas persegi kecil + (4 x luas segitiga siku-siku) = Luas persegi besar
(b – a) (b – a) + ( 4 x ½ x a x b) = c x c
b2 + a2 – 2ab + 2ab = c2
b2 + a2 = c2
atau dapat ditulis
a2 + b2 = c2
Keterangan:
a, b, c : ukuran sisi-segi segitiga/persegi.
Selanjutnya akan dibahas tentang tripel Pythagoras. Baca juga Persamaan Kuadrat.
Tripel Pythagoras
Apa itu tripel pythagoras?
Tripel pythagoras merupakan kombinasi tiga bilangan yang menyatakan ukuran segi-sisi segitiga siku-siku sehingga berlaku a2 + b2 = c2.
Berapa saja variasi dari tripel pythagoras?
Terdapat banyak sekali tripel pythagoras. Perhatikan beberapa tripel pythagoras berikut.
- Bilangan 3, 4, 5. Karena 32 + 42 = 52.
- Bilangan 5, 12, 13. Karena 52 + 122 = 132
- Bilangan 7, 24, 25. Karena 72 + 242 = 252.
- Bilangan 8, 15, 17. Karena 82 + 152 = 172.
- Bilangan 9, 40, 41. Karena 92 + 402 = 412.
Dan masih banyak tripel pythagoras yang yang lain.
Tripel pythagoras berlaku kelipatan, misalnya salah satu tripel pythagoras yaitu 3, 4, dan 5. Tripel pythagoras kelipatannya ialah (6, 8, 10), (9, 12, 15), (12, 16, 20), dan sebagainya.
Terdapat beberapa acuan soal pythagoras. Kerjakan soal berikut, kemudian cek jawabanmu dengan pembahasan yang ada.
Contoh Soal Pythagoras
1. Terdapat suatu segitiga siku-siku dengan ukuran dua segi yang berpenyiku yakni 21 cm dan 28 cm. Tentukan panjang segi yang yang lain.
Sisi yang dimaksud merupakan sisi miring segitiga siku-siku (hipotenusa).
Sehingga:
c2 = a2 + b2
= 212 + 282 = 441 + 784 = 1.225
c = √1.225 = 35 cm
Cara cepat:
Dengan menggunakan tripel (3, 4, 5) maka setiap sisi segitiga dikali dengan 7 sehingga
(3 x 7, 4 x 7, 5x 7) sehingga (21, 28, 35)
Panjang segi lainnya ialah 35 cm.
2. Terdapat segitiga siku-siku sama kaki dengan ukuran sisi miringnya yakni 5√2 cm. Tentukan panjang sisi yang yang lain.
Karena merupakan segitiga siku-siku sama kaki, maka panjang sisi yang berpenyiku sama. Sehingga:
Misalkan panjang segi berpenyiku yakni a, dab panjang sisi miring adalah c.
a2 + a2 = c2
2 x a2 = (5√2)2
2 x a2 = 50
a2 = 25
a = ± 5
Karena panjang sisi tidak mungkin negatif, maka panjang sisi berpenyiku adalah 5 cm.
3. Diketahui ukuran dua segi yang berpenyiku dari segitiga siku-siku adalah 12 cm dan 16 cm. Tentukan ukuran sisi yang yang lain.
Ukuran segi: 12 cm dan 16 cm
Ukuran segi ketiga
c2 = a2 + b2
c2 = 122 + 162
c2 = 144 + 256 = 400
c = √400 = 20 cm
4. Diketahui suatu bayangan menara mempunyai panjang 10 m, kalau jarak ujung menara dengan ujung bayangan menara yaitu 26 m, tentukan tinggi menara tersebut.
c2 = a2 + b2
b2 = c2 – a2
b2 = 262 – 102
b2 = 676 – 100
b2 = 576
b = √576 = 24 m
5. Tentukan apakah ukuran sisi-segi berikut merupakan tripel phytagoras.
12, 15,dan 20.
Sisi terpanjang: 20
Sehingga,
122 + 152 = 144+ 225 = 369
202 = 400
Karena 122 + 152 ≠ 202 maka 12, 15, dan 20 bukan tripel phytagoras.
Mari kita simpulkan bareng .
Kesimpulan
- Teorem pythagoras merupakan salah satu teorema atau aturan dalam matematika yang berhubungan dengan hubungan antar sisi segititas siku-siku.
- Teorema pythagoras menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat sisi-sisi yang yang lain.
Rumus teorema pythagoras yakni a2 + b2 = c2.
- Beberapa tripel pythagoras yakni (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), dan sebagainya. Tripel pythagoras berlaku kelipatannya.
Demikian pembahasan mengenai pythagoras dalam artikel ini, agar berfaedah. Baca juga Trigonometri.