x2 –
5x + 2y ≤ 1250
2x + 2y ≤ 800 –
3x ≤ 450
Sehingga nilai x yaitu 150. Total anggur dan beras ketan adalah 400, sedangkan jumlah angggur yakni 150, maka jumlah beras ketan ialah 250.
Program Linear: Pemahaman, Rumus, Contoh Soal
5. Jika diberikan sebuah fungsi f(x,y) = 4x + 5y pada grafik di bawah ini. Tentukan garis maksimum fungsi tersebut
Pembahasan
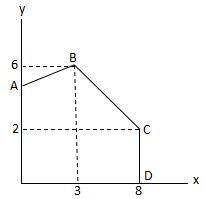
Pertama, kita harus menyaksikan titik-titik ekstrem pada gambar di atas. Sehingga di temukan titik ekstremnya ialah B(3,6), C(8,2), dan D(8,0).
Kemudian, kita masukkan titik ekstrem ini ke dalam persamaan f(x,y) = 4x + 5y.
Nilai paling besar ialah titik maksimumnya. Berdasarkan perkiraan, titik maksimum melintasi garis BC. Sehingga mampu disimpulkan bahwa BC ialah garis maksimum.
6. Pada gambaran berikut terdapat urusan terkait penumpang besawat, berat bagasi, dan harga tiket.
Dalam suatu pesawat terdapat 48 kawasan duduk penumpang. Setiap penumpang kelas utama maksimum menjinjing 60 kg bagasi, sedangkan penumpang kelas ekonomi cuma diperbolehkan menjinjing bagasi maksimal 20 kg. Pesawat tersebut cuma bisa memuat total bagasi penumpang maksimum 1440 kg. Jika harga tiket penumpang kelas utama adalah Rp1.500.000,00 dan penumpang kelas ekonomi yakni Rp1.000.000,00, pastikan banyaknya daerah duduk kelas utama dan kelas ekonomi agar pendapatan dari penjualan tiket tersebut maksimum.
Pembahasan
Misalkan variabel-variabel kendala dimisalkan sebagai berikut.
- x : banyaknya penumpang kelas utama
- y : banyaknya penumpang kelas ekonomi
Menentukan fungsi tujuan:
Fungsi tujuan dari permasalahan tersebut ialah menentukan pemasukan maksimum:
z = 1.500.000 x + 1.000.000 y
Menyusun model dari variabel-variabel hambatan:
Banyak kawasan duduk maksimum adalah 48.
Banyak bagasi maksimum 60 kg (kelas utama) dan 20 kg (kelas ekonomi) dengan total bagasi maksimum 1.440 kg.
Sehingga
x + y ≤ 48
60 x + 20 y ≤ 1.440
Grafik dari fungsi tersebut:
x + y ≤ 48
| x | 48 | 0 |
| y | 0 | 48 |
Titik yang dilalui garis ialah (48, 0) dan (0, 48)
60 x + 20 y ≤ 1440
| x | 24 | 0 |
| y | 0 | 72 |
Titik-titik yang dilalui garis yakni (24, 0) dan (0, 72)
Gambar grafik fungsi kendala ialah sebagai berikut.
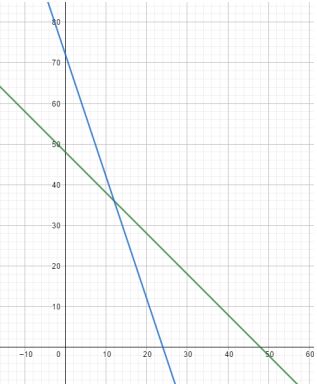
Menentukan titik potong kedua grafik.
Dengan memakai rancangan SPLDV diperoleh
x + y = 48 à y = 48 – x
60 x + 20 y = 1.440
Sehingga
60 x + 20 (48 – x) = 1.440
60x + 960 – 20x = 1.440
40x = 1.440 – 960
40 x = 480
x = 480/40 = 12
x + y = 48
x = 12 à y = 48 – 12 = 36
Titik potong kedua garis pada (12, 36)
Menentukan tempat solusi.
Perhatikan kawasan penyelesaian berikut.
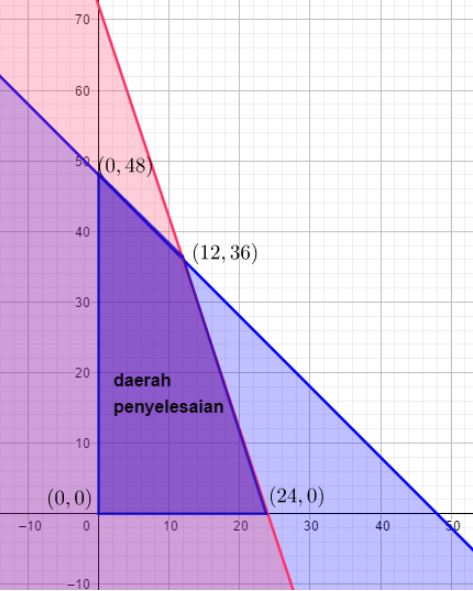
Pada gambar tersebut terdapat kawasan penyelesaian yang berwarna ungu. Langkah berikutnya adalah menghitung nilai optimum dari fungsi tujuan.
Titik optimumnya adalah (0, 0), (24, 0), (12, 36), dan (0, 48).
Fungsi tujuan: z = 1.500.000 x + 1.000.000 y
(0, 0) à z = 1.500.000 (0) + 1.000.000 (0) = 0
(24, 0) à z = 1.500.000 (24) + 1.000.000 (0) = 36.000.000
(12, 36) à z = 1.500.000 (12) + 1.000.000 (36) = 18.000.000 + 36.000.000 = 54.000.000
(0,48) à z = 1.500.000 (0) + 1.000.000 (48) = 48.000.000
Maksimum pemasaran tiket yakni 54.000.000
Kaprikornus, supaya penjualan tiket maksimum maka banyaknya penumpang kelas utama ialah 12 penumpang dan banyaknya penumpang kelas ekonomi adalah 36 penumpang.
Kesimpulan
- Program linear merupakan salah satu teknik optimasi yang dipakai dalam aneka macam bidang untuk memilih optimalisasi sebuah kegiatan (misalnya produksi, penjualan, dan lain-lain).
- Langkah-langkah penghitungan dengan menggunakan acara linear yaitu menentukan variabel kendala, menyusun fungsi tujuan, menyusun model, menggambar grafik model, menentukan titik potong grafik, memilih tempat penyelesaian, dan memilih nilai optimum dari fungsi tujuan.
Demikian pembahasan perihal program linear. Semoga bermanfaat bagi pembaca seluruhnya. Baca juga Persamaan Linear.