Daftar Isi
Pengertian Persamaan irasional
Persamaan irasional adalah suatu persamaan yang mengandung atau memuat variabel yang berada di dalam tanda akar. Agar lebih jelas perhatikan contoh-contoh dibawah ini:
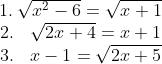
Tiga contoh soal diatas merupakan contoh persamaan irasional, karena variabel-variabelnya berada didalam tanda akar.
Soal-soal dibawah ini bukan persamaan irasional , karena karena variabelnya tidak berada dalam tanda akar, walaupun persamaan tersebut mengandung tanda akar.
Tiga contoh soal diatas merupakan contoh persamaan irasional, karena variabel-variabelnya berada didalam tanda akar.
Soal-soal dibawah ini bukan persamaan irasional , karena karena variabelnya tidak berada dalam tanda akar, walaupun persamaan tersebut mengandung tanda akar.
Agar tidak terjadi miskonsepsi , maka definisi diatas haruslah benar-benar dipahami.
Bentuk Umum Persamaan irasional
Secara umum berbentuk seperti dibawah ini:
f(x) dan g(x) merupakan suatu polinomial (suku banyak).
Himpunan Penyelesaian Persamaan irasional
Jika kita melakukan subtitusi kedalam persamaan irasional akan memberikan pernyataan yang benar maka inilah yang disebut Himpunan Penyelesaian .
Cara menyelesaikannya adalah dengan menghilangkan tanda akarnya terlebih dahulu, yaitu dengan cara mengkuadratkan ruas kiri dan ruas kanannya. Proses mengkuadratkan tersebut dapat dilakukan berulang kali, sampai tanda akarnya hilang dan diperoleh persamaan baru yang ekivalen.
Secara umum prinsipnya adalah:
})^{2}=\left&space;(&space;g(x)&space;\right&space;)^{2}\,&space;atau\,&space;\left&space;(&space;\sqrt{f(x)}&space;\right&space;)^{2}=\left&space;(&space;\sqrt{g(x)}&space;\right&space;)^{2}\,&space;....(1)\\Dengan&space;\,&space;prasyarat:\\\Leftrightarrow&space;f(x)\geq&space;0\,&space;.....(2)\\\Leftrightarrow&space;g(x)\geq&space;0\,&space;.....(3))

Maka Himpunan penyelesaian persamaan irasional yang dimaksud adalah penyelesaian yang memenuhi (1),(2),dan (3). Agar lebih jelas perhatikan contoh-contoh dibawah ini:
Contoh 1:
Selesaikanlah Persamaan irasional,
Selesaikanlah Persamaan irasional,
[solusi]
Tentukan terlebih dahulu prasyarat, yaitu:
Tentukan terlebih dahulu prasyarat, yaitu:
Selanjutnya selesaikan :
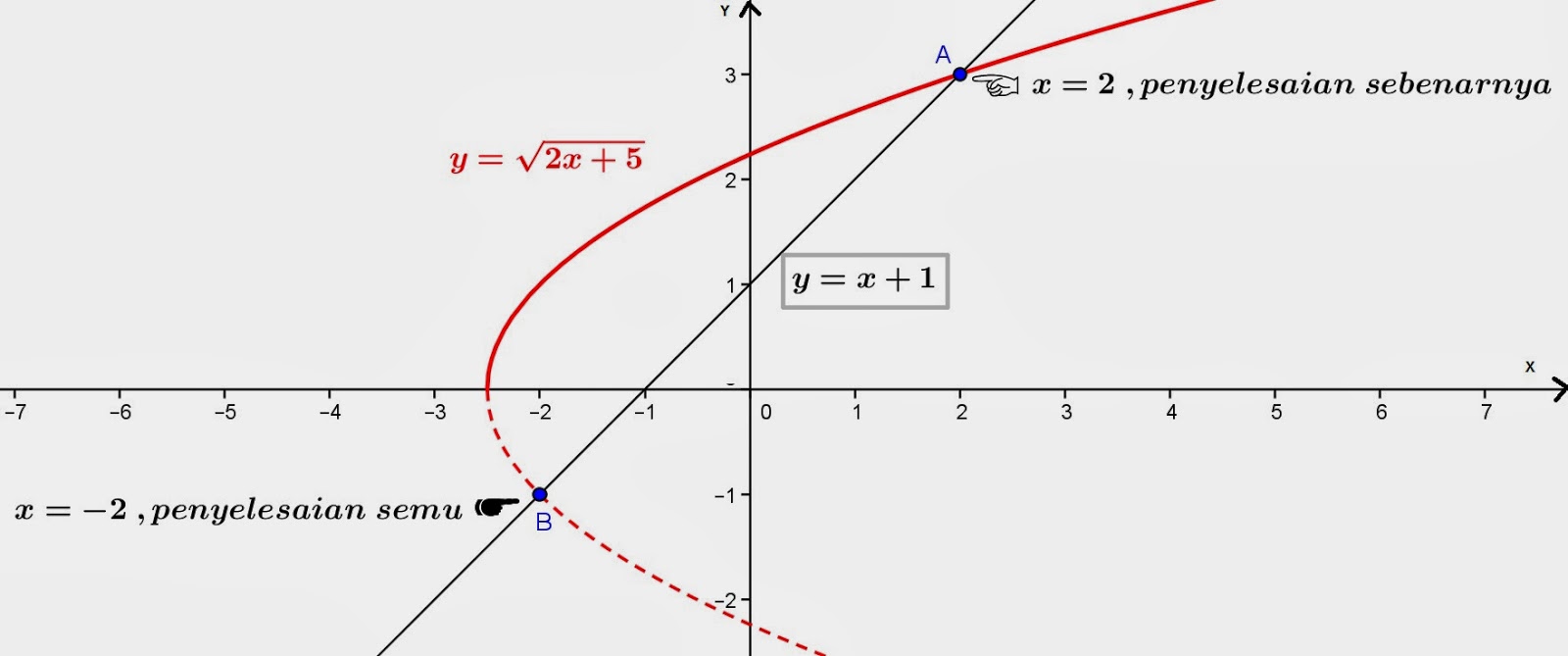
Secara grafis persamaan diatas dapat di gambarkan sebagai berikut:
Dari grafik diatas, tampak bahwa kedua grafik berpotongan di titik A dan titik B. Maka himpunan penyelesaiannya adalah adalah titik A, yaitu x = 2 (bagian yang bergaris tebal). Dan titik B, yaitu x = -2 adalah penyelesaian semu (bagian yang bergaris putus-putus).
Contoh 2:
Selesaikanlah Persamaan irasional berikut ini,
[Solusi]
Tentukan terlebih dahulu Prasyarat :
\\\\5-x\geq&space;0\Rightarrow&space;x\leq&space;5\,&space;.....(2)\\\\dari\,&space;(1)\,&space;dan\,&space;(2):0\leq&space;x\leq&space;5\,&space;.....(3))
Selanjutnya selesaikan :
^{2}=\left&space;(&space;\sqrt{5-x}&space;\right&space;)^{2}\\\\\Leftrightarrow&space;x-2\sqrt{x}+1=5-x\\\\\Leftrightarrow&space;2x-4=2\sqrt{x}\\\\\Leftrightarrow&space;x-2=\sqrt{x}\,&space;(kuadratkan\,&space;kedua\,&space;ruas))
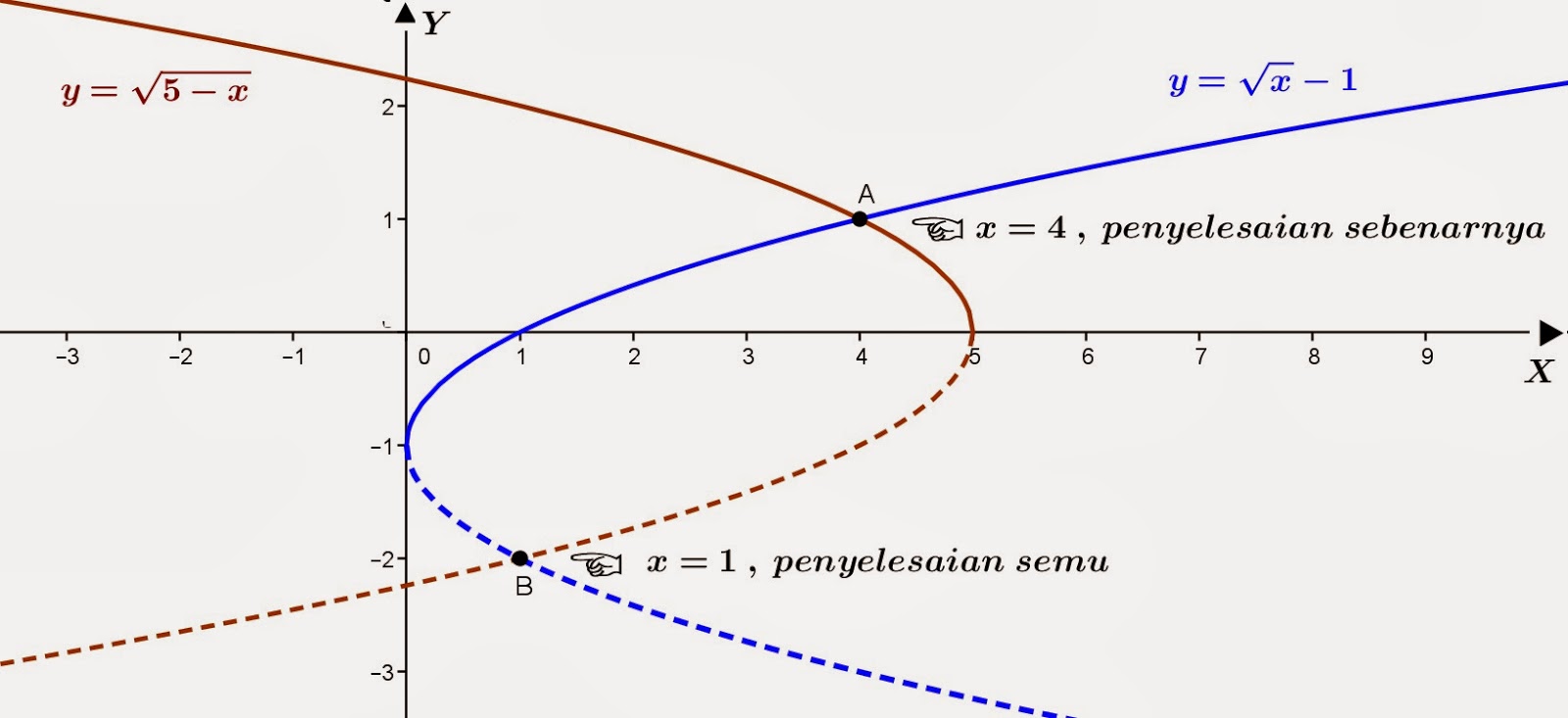
^{2}=(\sqrt{x})^{2}\\\\x^2-5x+4=0\Leftrightarrow&space;(x-4)(x-1)=0\\\\x=1\,&space;atau\,&space;x=4\,&space;\therefore&space;dari&space;syarat\,&space;(3):\,&space;{\color{Red}&space;x=4})
Penyelesaian dengan grafik, yaitu sebagai berikut:
Contoh 3:
Tentukan himpunan penyelesaian dari Persamaan irasional berikut ini , [Solusi]Tentukan terlebih dahulu prasyarat :
Selanjutnya selesaikan:
Jadi, persamaan rasional,
tidak mempunyai solusi.
Ada cara lain dalam menentukan himpunan penyelesaian persamaan irasional, yaitu dengan mensubtitusikan kembali nilai x yang diperoleh kedalam persamaan semula, jika hasilnya ruas kiri sama dengan ruas kanan maka nilai tersebut adalah penyelesaianya.
Perhatikan contoh dibawah ini!
Contoh 4 :
Tentukan himpunan penyelesaian dari,
[Penyelesaian]
(x+2)=0\\\\\therefore&space;x=3\,&space;atau\,&space;x=-2)
Subtitusikan x = 3 dan x = -2 ke persamaan semula,
\\\\\therefore&space;x=3\,&space;adalah\,&space;penyelesaian)
^2-4}=\sqrt{-2+2}\\\\\Leftrightarrow&space;0=0\,&space;(ruas\,&space;kiri\,&space;sama\,&space;dengan\,&space;ruas\,&space;kanan)\\\\\therefore&space;x=-2,\,&space;adalah\,&space;penyelesaian)
Jadi, himpunan penyelesainnya adalah { 3 , – 2}
Dari contoh-contoh diatas dapat disimpulkan bahwa, persamaan irasional bisa mempunyai penyelesaian atau bisa juga tidak mempunyai penyelesaian. Sebagai latihan cobalah selesaikan, soal-soal dibawah ini.
Selesaikan Persamaan irasional dibawah ini !
Kunci Jawaban
Penerapan persamaan irasional dalam kehidupan sehari-hari
Dalam kehidupan sehari-hari tentu kita terkadang dihadapkan pada permasalahan, yang dapat diselesaikan dengan menggunakan prinsip-prinsip menyelesaikan persamaan irasional. Salah satu contohnya seperti dibawah ini:
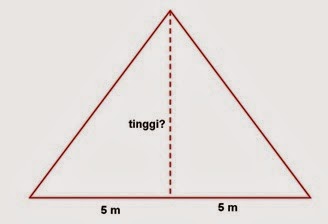
Seorang arsitek akan membuat kuda-kuda suatu atap rumah dari kayu balok dengan lebarnya 10 m. Perhatikan gambar dibawah ini:
Untuk membuat satu buah kuda-kuda seperti gambar diatas ditetapkan hanya 26 meter. Berapakah tinggi kuda-kuda atap rumah tersebut ?
[Penyelesaian]
Permasalahan diatas dapat digambarkan seperti dibawah ini,
Maka dapat dibentuk persamaan irasional yaitu :
Jadi tinggi kuda-kuda tersebut agar balok kayu yang tersedia mencukupi adalah 3,64 meter.
Membutuhkan banyak latihan dan pemahaman konsep yang baik ya, agar bisa paham persamaan irasional, yang nantinya akan menjadi dasar dalam mempelajari materi lain seperti pertidaksamaan nilai mutlak, persamaan nilai mutlak dan pertidaksamaan linier satu variariabel.
Tentu masih banyak permasalahan dalam kehidupan sehari-hari yang dapat diselesaikan dengan prinsip-prinsip persamaan irasional .