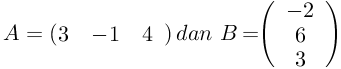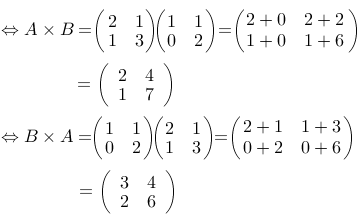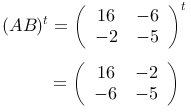Perkalian Matriks – Media Masyarakat

Daftar Isi

Sifat-sifat Operasi dan Syarat-syarat perkalian matriks matematika

Perkalian matriks terhadap matriks lain serta syarat-syarat apa saja yang harus dipenuhi agar hasil perkalian matriks tersebut terdefinisi, akan dibahas pada materi ini sebaiknya pelajari terlebih dahulu materi prasyarat tentang dasar-dasar matriks, agar anda lebih mudah mempelajari materi perkalian matriks ini.

Syarat-syarat Perkalian matriks

(a) Hasil perkalian matriks A dan B dengan ordo $A_{1\times m}\, \, dan\, \, B_{m\times 1}$ adalah matriks $C_{1\times 1}$ dimana elemen pada baris ke-1 dan kolom ke-1 merupakan jumlah dari perkalian elemen-elemen yang bersesuaian pada baris ke-1 matriks A dan kolom ke-1 matriks B

http://soulmath4u.blogspot.com/2014/03/perkalian-matriks.html

Contoh:

Hitunglah perkalian matriks dibawah ini!

Hitunglah A× B

[Penyelesaian]

Sesuai dengan prinsip perkalian matriks , maka

(b). Perkalian matriks $A_{m\times n}$ dengan matriks $B_{p\times q}$ terdefinisi jika n = p atau Jika banyaknya kolom matriks A sama dengan banyaknya baris pada matriks B. Dan hasil kali nya adalah matriks $C_{m\times q}$

Pengertian dikalikan dari kiri dan dikalikan dari Kanan dalam Perkalian Matriks

Dalam perkalian dua matriks tidak berlaku sifat komutatif, AB ≠ BA. Dalam aljabar perkalian matriks AB disebut matriks B dikalikan dari kiri oleh matriks A dan perkalian matriks BA disebut matriks B dikalikan dari kanan oleh matriks A.

Perhatikan contoh dibawah ini!

Diketahui dua buah matriks dibawah ini:

Apakah AB = BA?

[Penyelesaian]

Hasil kali AB dan BA seperti dibawah ini,

Dari hasil diatas maka AB ≠ BA.

Pemangkatan Matriks Persegi

Jika A suatu matriks persegi, maka berlaku seperti dibawah ini,

Sifat-sifat Operasi perkalian Matriks

Jika setiap perkalian matriks A dan B terdefinisi, maka selalu berlaku:

1) (AB)C = A(BC) , (sifat asosiatif)

2) A(B + C) = AB + AC, (sifat distributif kiri)

3) (B + C)A= BA + CA , (sifat distributif kanan)

4) k (AB) = (kA)B= A(kB), k skalar dan k ϵ R

Sifat-sifat Operasi Transpose pada Matriks

Dibawah ini sifat-sifat transpose pada matriks,

Contoh Soal perkalian matriks dengan matriks

Dibawah ini contoh-contoh soal dan penerapan sifat-sifat operasi perkalian matriks

Selesaikan soal-soal dibawah ini!

(1). Diketahui Matriks-matriks dibawah ini, Hitunglah A × B ,

[Penyelesaian]

Sesuai dengan prinsip perkalian matriks, maka

(2). Hitunglah perkalian matriks ordo 2× 2dibawah ini,

[Penyelesaian]

(3). Hitunglah perkalian matriks 3 × 3 dibawah ini

[Penyelesaian]

Solusi perkalian matriks 3 × 3 diatas adalah,

(4). Hitunglah perkalian matriks beda ordo B dan C berikut ini,

Contoh Soal Limit

[Penyelesaian]

Matriks $B_{2\times 2}\, \, dan\, \, C_{2\times 3}$ , banyak kolom matriks B sama dengan banyak baris matriks C maka B × C terdefinisi. Hasil perkaliannya adalah,