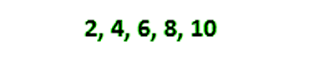KURIKULUM PELAJARANCG : Statistik yakni cabang matematika yang berhubungan dengan pengumpulan, interpretasi, pengorganisasian, dan interpretasi data. Awalnya, dikala kita menerima data, alih-alih menerapkan algoritma terbaik dan menciptakan beberapa prediksi, pertama-tama kita mencoba membaca dan mengetahui data dengan menerapkan teknik statistik. Dengan melaksanakan ini, kita mampu mengetahui jenis data distribusi apa yang dimiliki.
Setiap pelajar / siswa statistik mesti tahu wacana banyak sekali cabang statistik untuk memahami statistik dengan benar dari sudut pandang yang lebih holistik. Seringkali, jenis pekerjaan atau penelitian yang terlibat dalam menyembunyikan aspek statistik yang lain, tetapi sangat penting untuk mengenali ide keseluruhan di balik analisis statistik untuk sepenuhnya menghargai kepentingan dan keindahannya.
Dua cabang utama Ilmu statistik yaitu statistik deskriptif dan statistik inferensial. Keduanya dipakai dalam analisis data ilmiah dan keduanya sama pentingnya bagi pelajarancg matematika khususnya siswa statistik. Lalu apa itu statistik dalam arti Statistik dari jenis deskriptif dan Inferensial, berikut klarifikasi pelajarancg.blogspot.com:
Daftar Isi
PENGERTIAN STATISTIK DAN STATISTIKA
Menurut para hebat dalam buku Nar Herrhyanto dan H.M. Akib Hamid berpendapat bahwa Pengertian Statistik ialah kata statistik dapat diartikan selaku suatu ukuran yang dihitung dari sekumpulan data dan ialah wakil dari data itu. Sedangkan pemahaman Statistika dalam buku Richard A. Johnson dan Gouri K. Bhattacharya berpendapat bahwa Pengertian Statistika adalah selaku subjek menawarkan badan dari prinsip dan metodologi untuk mendesain proses pengumpulan data, meringkas dan menafsirkan data, dan menawan kesimpulan atau generalisasi.
Dari pendapat para spesialis atau ahli diatas dapat ditarik kesimpulan bahwa statistik ialah data hasil dari observasi yang telah tersedia dalam bentuk tabel, atau grafik, misalnya 80% mahasiswa yang mengikuti kuliah yaitu perempuan atau rata-rata nilai ulangan matematika siswa satu kelas adalah sedangkan statistika lebih mengarah kepada prinsip dan metodologi yang dipakai untuk mendapatkan data statistik tersebut.
Untuk membedakan pendefinisian antara statistika dan statistika dalam matematika maupun bidang keilmuan lainnya, berikut klarifikasi pelajarancg.blogspot.com
Arti Statistik
Kata statistik (Inggris: Statistic) bukan merupakan kata dari bahasa Indonesia asli, secara etimologis kata “statistik” berasal dari kata status (bahasa latin) yang memiliki persamaan arti dengan kata state (bahasa Inggris) atau kata staat (bahasa Belanda), dan yang dalam bahasa Indonesia diterjemahkan menjadi negara. Pada mulanya, kata “statistik” diartikan sebagai “kumpulan materi keterangan (data), baik yang berwujud angka (data kuantitatif) maupun yang tidak berwujud angka (data kualitatif), yang mempunyai arti penting dan kegunaan yang besar bagi suatu negara. Namun, pada kemajuan berikutnya, arti kata statistik hanya dibatasi pada “kumpulan materi keterangan yang berwujud angka (data kuantitatif)” saja; bahan informasi yang tidak berwujud angka (data kualitatif) tidak lagi disebut statistik.
Seiring berjalannya waktu kata statistic tidak lagi dibatasi untuk kepentingan-kepentingan Negara saja namun sudah digunakan dalam keseharian untuk mempermudah penduduk untuk menganalisis sesuatu yang berkaitan dengan data-data. Sehingga setelah masyarakat memahami statistic dan mulai mempergunakannya dalam kehidupan sehari munculah berbagai jenis dari macam-macam nama statistik. Statistik yang menjelaskan sesuatu hal biasanya diberi nama statistik mengenai hal yang bersangkutan didalamnya, misalnya kumpulan data yang membicarakan wacana tingkat bikinan suatu perusahaan dinamakan statistik buatan. Banyak masalah baik itu seperti observasi ataupun pengamatan yang dinyatakan dalam bentuk bilangan atau angka-angka. Kumpulan angka-angka disusun atau dikelola dan disajikan dalam tabel terkadang dilengkapi dengan gambar baik berbentukdiagram maupun grafik, hal ini dikerjakan bermaksud untuk membuat lebih mudah menerangkan isi dari data.
Pengertian Statistika
Menurut Wikipedia, Statistika adalah ilmu yang mempelajari bagaimana mempersiapkan, menghimpun, menginterpretasi, menganalisis, dan mempresentasikan data. Singkatnya, statistika yaitu ilmu yang berkenaan dengan data. Istilah ‘statistika’ (bahasa Inggris: statistics) berlawanan dengan ‘statistik’ (statistic). Secara lazim Statistika merupakan ilmu yang berkenaan dengan data, sedang statistik adalah data, gosip, atau hasil penerapan algoritme statistika pada sebuah data. Dari kumpulan data, statistika mampu digunakan untuk menyimpulkan atau mendeskripsikan data; ini dinamakan statistika deskriptif. Sebagian besar desain dasar statistika mengasumsikan teori probabilitas. Beberapa ungkapan statistika antara lain: populasi, sampel, unit sampel, dan probabilitas.
Pelajarancg Statistika banyak dipraktekkan dalam aneka macam disiplin ilmu, baik ilmu-ilmu alam (contohnya astronomi dan biologi maupun ilmu-ilmu sosial (tergolong sosiologi dan psikologi), maupun di bidang bisnis, ekonomi, dan industri. Statistika juga dipakai dalam pemerintahan untuk banyak sekali macam tujuan; sensus penduduk ialah salah satu prosedur yang paling dikenal. Aplikasi statistika yang lain yang kini popular yakni mekanisme jajak usulan atau polling (contohnya dilakukan sebelum pemilihan umum), serta hitung cepat (perkiraan cepat hasil pemilu) atau quick count. Di bidang komputasi, statistika dapat pula dipraktekkan dalam pengenalan acuan maupun kecerdasan buatan.
PENGERTIAN STATISTIK DESKRIPTIF DAN STATISTIK INFERENSIAL DALAM METEMATIKA
Statistik deskriptif (deduktif) berhubungan dengan presentasi dan pengumpulan data. Ini umumnya merupakan bagian pertama dari analisis statistik. Dari kesimpulan pertimbangan para andal berpendapat, Statistik Deskriptif (deduktif) atau sederhana yaitu statistik yang tingkat pengerjaannya mencakup cara-cara mengkalkulasikan, menyusun atau menertibkan, mengolah, menghidangkan, dan menganalisa data semoga dapat menunjukkan gambaran yang ringkas tentang suatu keadaan lazimnya tidak sesederhana kedengarannya, dan hebat statistik perlu menyadari mendesain eksperimen, memilih kelompok fokus yang sempurna dan menghindari bias yang begitu mudah untuk masuk ke dalam eksperimen.
Pelajaran studi matematika yang berlainan membutuhkan jenis analisis yang berlawanan memakai statistik deskriptif. Misalnya, seorang ahli fisika yang mempelajari turbulensi di laboratorium membutuhkan jumlah rata-rata yang beraneka ragam dalam interval waktu yang kecil. Sifat masalah ini mensyaratkan bahwa jumlah fisik dirata-rata dari sejumlah data yang dikumpulkan melalui percobaan.
Dari dua cabang utama Pelajaran studi Ilmu statistik adalah terbagi menjadi dua dari macam-macam nama statistik (deskriptif dan inferensial).
PENGERTIAN DARI STATISTIK DESKRIPTIF
Statistik deskriptif melibatkan ringkasan dan pengorganisasian data sehingga mudah diketahui. Statistik deskriptif, berbeda dengan statistik inferensial, berusaha menggambarkan data, tetapi jangan mencoba menciptakan kesimpulan dari sampel ke seluruh populasi. Di sini, kami umumnya menggambarkan data dalam sampel. Ini lazimnya bermakna bahwa statistik deskriptif, tidak mirip statistik inferensial, tidak dikembangkan menurut teori probabilitas.
Statistik deskriptif (deduktif) berkaitan dengan presentasi dan pengumpulan data. Ini biasanya merupakan bagian pertama dari analisis statistik. Dari kesimpulan pendapat para ahli berpendapat, Statistik Deskriptif (deduktif) atau sederhana yakni statistik yang tingkat pengerjaannya mencakup cara-cara menghitung, menyusun atau mengontrol, mengolah, menyajikan, dan mengevaluasi data supaya mampu menawarkan citra yang ringkas mengenai sebuah kondisi lazimnya tidak sesederhana kedengarannya, dan mahir statistik perlu menyadari merancang eksperimen, menentukan kalangan konsentrasi yang sempurna dan menyingkir dari bias yang begitu mudah untuk masuk ke dalam eksperimen.
Wilayah studi yang berlainan membutuhkan jenis analisis yang berlainan memakai statistik deskriptif. Misalnya, spesialis fisika yang mempelajari turbulensi di laboratorium membutuhkan jumlah rata-rata yang bermacam-macam dalam interval waktu yang kecil. Sifat masalah ini mensyaratkan bahwa jumlah fisik dirata-rata dari sejumlah data yang dikumpulkan melalui percobaan.
Kecenderungan sentral mengacu pada ide bahwa ada satu angka yang paling baik merangkum seluruh rangkaian pengukuran, sebuah angka yang dalam beberapa cara pengukuran “sentral” ke set. Sebagai contoh:
Mean / rata-rata
Mari kita hitung rata-rata (mean) atau dikenal dengan average dengan kumpulan data yang mempunyai 8 bilangan lingkaran. Mean atau Rata-rata ialah kecenderungan sentral dari data ialah angka di mana seluruh data tersebar. Di satu segi, mean ialah angka tunggal yang dapat memperkirakan nilai seluruh kumpulan data.
Mari kita hitung mean dari kumpulan data yang memiliki 8 bilangan bulat.
 |
| Gambar: Contoh perkiraan mean atau average |
Median
Median yaitu nilai yang membagi data dalam 2 bagian yang sama ialah jumlah ungkapan di segi kanan sama dengan jumlah ungkapan di sisi kiri dikala data disusun dalam urutan naik atau turun.
Catatan: Jika Kita mengurutkan data dalam urutan menurun, itu tidak akan memengaruhi median tetapi IQR akan negatif. Kita akan berbicara wacana IQR nanti di blog pelajarancg.blogspot.com.
Median akan menjadi jangka menengah, bila jumlah istilahnya ganjil
Median akan menjadi rata-rata dari 2 istilah tengah, bila jumlah istilahnya genap.
 |
| Gambar: Contoh perhitungan median |
Median ialah 59 yang hendak membagi set angka menjadi dua bagian yang serupa. Karena ada angka genap dalam set, jawabannya yaitu rata-rata angka tengah 51 dan 67.
Catatan: Ketika nilai berada dalam progresi aritmatika (perbedaan antara suku-suku berturut-turut yakni konstan. Ini 2.), median selalu sama dengan mean.
Rata-rata/ mean dari 5 angka ini yaitu 6 dan lebih median.
Mode
Mode adalah istilah yang muncul waktu maksimum dalam kumpulan data yaitu perumpamaan yang memiliki frekuensi tertinggi.
 |
| Gambar: Contoh perhitungan mode |
Dalam kumpulan data ini, mode yaitu 67 alasannya mempunyai lebih dari sisa nilai, contohnya dua kali.
Tetapi mungkin ada kumpulan data di mana tidak ada mode sama sekali alasannya adalah semua nilai muncul jumlah yang sama kali. Jika dua nilai muncul waktu yang sama dan lebih dari sisa nilai maka set data yakni bimodal. Jika tiga nilai muncul waktu yang serupa dan lebih dari sisa nilai maka set data yaitu trimodal dan untuk mode n, set data tersebut multimodal.
JENIS-JENIS DARI STATISTIK DESKRIPTIF
Statistik deskriptif memungkinkan kita untuk mengkarakterisasi data kita berdasarkan propertinya. Ada empat jenis utama statistik deskriptif:
- Ukuran Frekuensi:
- Hitung, Persen, Frekuensi
- Menunjukkan seberapa sering sesuatu terjadi
- Gunakan ini saat Kita ingin memperlihatkan seberapa sering respons diberikan
- Ukuran Tendensi Sentral
- Berarti, Median, dan Mode
- Menempatkan distribusi dengan berbagai titik
- Gunakan ini ketika Kita ingin menawarkan bagaimana tanggapan rata-rata atau paling biasa ditunjukkan
- Ukuran Dispersi atau Variasi
- Rentang, Varian, Deviasi Standar
- Mengidentifikasi sebaran skor dengan menyatakan interval
- Rentang = Tinggi / Rendah poin
- Varians atau Standar Deviasi = perbedaan antara skor yang diperhatikan dan rata-rata
- Gunakan ini ketika Kita ingin memberikan seberapa “menyebar” data tersebut. Sangat menolong untuk mengenali kapan data Kita tersebar sedemikian sehingga memengaruhi rata-rata
- Ukuran Posisi
- Peringkat Persentil, Peringkat Kuartil
- Menjelaskan bagaimana skor jatuh dalam kekerabatan satu sama lain. Bergantung pada skor kriteria
- Gunakan ini saat Kita perlu membandingkan skor dengan skor yang dinormalisasi (misalnya., Norma nasional)
PENGERTIAN DARI STATISTIK INFERENSIAL
Statistik deskriptif menggambarkan data (contohnya, bagan atau grafik) dan statistik inferensial memungkinkan kita membuat prediksi (“kesimpulan”) dari data itu. Dengan statistik inferensial, kita mengambil data dari sampel dan menciptakan generalisasi perihal suatu populasi. Misalnya, kita mungkin bangkit di mal dan meminta sampel 100 orang kalau mereka suka membeli di . Kita mampu menciptakan diagram batang balasan ya atau tidak (yang akan menjadi statistik deskriptif) atau Kita dapat memakai penelitian kita (dan statistik inferensial) untuk argumentasi bahwa sekitar 75-80% populasi (semua pembeli di semua mal) suka berbelanja di .
Statistik inferensial adalah seperti namanya, melibatkan penarikan kesimpulan yang sempurna dari analisis statistik yang telah dilaksanakan memakai statistik deskriptif. Pada jadinya, itu yaitu kesimpulan yang menciptakan studi penting dan aspek ini ditangani dalam statistik inferensial.
Sebagian besar prediksi abad depan dan generalisasi wacana populasi dengan mempelajari sampel yang lebih kecil berada di bawah bidang statistik inferensial. Sebagian besar eksperimen ilmu sosial bermasalah dengan mempelajari populasi sampel kecil yang menolong memilih bagaimana populasi secara umum berperilaku. Dengan merancang eksperimen yang tepat, peneliti dapat menawan kesimpulan yang berhubungan dengan studinya.
Saat menggambar kesimpulan, seseorang mesti sangat waspada supaya tidak mempesona kesimpulan yang salah atau bias. Meskipun ini terlihat seperti sebuah sains, ada cara di mana seseorang dapat memanipulasi studi dan hasil lewat aneka macam cara. Sebagai acuan, pengerukan data semakin menjadi persoalan alasannya adalah komputer menyimpan banyak isu dan gampang, baik secara sengaja atau tidak, menggunakan tata cara inferensial yang salah.
Statistik deskriptif dan inferensial berlangsung beriringan dan satu tidak dapat ada tanpa lainnya. Metodologi ilmiah yang baik perlu disertai dalam kedua langkah analisis statistik ini dan kedua cabang statistik ini sama pentingnya bagi seorang peneliti.
JENIS-JENIS DARI STATISTIK INFERENSIAL
Statistik Inferensial memungkinkan kita untuk menciptakan prediksi (“kesimpulan”). Ada dua jenis utama statistik inferensial:
- Memperkirakan parameter. Ini memiliki arti mengambil statistik dari data sampel Kita (misalnya mean sampel) dan menggunakannya untuk menyampaikan sesuatu ihwal parameter populasi (mis. Mean populasi).
- Tes hipotesis. Di sinilah Kita mampu menggunakan data sampel untuk menjawab pertanyaan penelitian. Misalnya, Kita mungkin kesengsem mengenali apakah obat kanker baru efektif. Atau jika sarapan membantu anak-anak tampil lebih baik di sekolah.
Katakanlah Kita mempunyai beberapa sampel data ihwal obat kanker gres yang berpotensi. Kita mampu memakai statistik deskriptif untuk menggambarkan sampel kita, tergolong:
- Rata-rata sampel
- Contoh patokan deviasi
- Membuat skema batang atau plot kotak
- Menjelaskan bentuk distribusi probabilitas sampel
Dengan statistik inferensial, Kita mengambil data sampel dari sejumlah kecil orang dan dan mencoba menentukan apakah data tersebut dapat memprediksi apakah obat akan bekerja untuk siapa saja (yaitu populasi). Ada berbagai cara kita mampu melakukan ini, mulai dari mengkalkulasikan skor-z (skor-z yaitu cara untuk menunjukkan di mana data kita akan berada dalam distribusi normal sampai pengujian pasca-hoc (lanjutan).
Statistik inferensial menggunakan versi statistik untuk menolong Kita membandingkan data sampel kita dengan sampel lain atau dengan penelitian sebelumnya. Sebagian besar observasi menggunakan model statistik yang disebut model Generalized Linear dan ANOVA (Analysis of Variance), analisis regresi dan banyak sekali model lainnya yang menciptakan probabilitas dan hasil garis lurus (“linear”).
Prinsip utama untuk statistik inferensial adalah:
- Teorema Binomial
- Pengujian Hipotesis
- Distribusi Normal
- Distribusi-T
- Teorema Batas Pusat
- Interval Keyakinan
- Analisis Regresi / Regresi Linier
- Perbandingan Sarana.
KESIMPULAN PELAJARAN METEMATIKA STATISTIK : PENGERTIAN STATISTIK DESKRIPTIF DAN STATISTIK INFERENSIAL
Apa persamaan antara statistik deskriptif dan inferensial?
Statistik deskriptif dan inferensial bergantung pada set data yang sama. Statistik deskriptif hanya mengandalkan kumpulan data ini, sementara statistik inferensial juga bergantung pada data ini untuk menciptakan generalisasi tentang populasi yang lebih besar.
Apa kekuatan memakai statistik deskriptif untuk mengusut distribusi skor?
Selain kejelasan statistik deskriptif yang mampu memperjelas volume data yang besar, tidak ada ketidakpastian perihal nilai yang Kita dapatkan (selain cuma kesalahan pengukuran, dll.).
Apa keterbatasan statistik deskriptif?
Statistik deskriptif sungguh terbatas sehingga mereka cuma memungkinkan Kita untuk menciptakan penjumlahan ihwal orang atau objek yang sudah Kita ukur. Kita tidak dapat menggunakan data yang sudah Kita kumpulkan untuk digeneralisasi ke orang atau objek lain (contoh studi, Menggunakan data dari sampel untuk menyimpulkan properti / parameter populasi). Misalnya, bila Kita menguji obat untuk mengalahkan kanker dan itu bekerja pada pasien Kita, Kita tidak mampu mengklaim bahwa itu akan bekerja pada pasien kanker lainnya hanya mengandalkan statistik deskriptif (namun statistik inferensial akan memberi Kita kesempatan ini).
Apa keterbatasan statistik inferensial?
Ada dua batasan utama untuk penggunaan statistik inferensial. Keterbatasan pertama, dan yang paling penting, yang ada dalam semua statistik inferensial, ialah bahwa Kita memberikan data perihal populasi yang belum sepenuhnya diukur, dan oleh alasannya itu, tidak pernah mampu sepenuhnya yakin bahwa nilai / statistik yang Kita hitung benar. Ingat, statistik inferensial didasarkan pada konsep menggunakan nilai yang diukur dalam sampel untuk memperkirakan / menyimpulkan nilai yang hendak diukur dalam suatu populasi; akan senantiasa ada tingkat ketidakpastian dalam melakukan ini. Batasan kedua terhubung dengan batas-batas pertama. Beberapa, tetapi tidak semua, tes inferensial mewajibkan pengguna (mis., Kita ) untuk membuat tebakan yang dididik (menurut teori) untuk menjalankan tes inferensial. Sekali lagi, akan ada beberapa ketidakpastian dalam proses ini, yang mau berdampak pada kepastian hasil dari beberapa statistik inferensial. demikian dari Statistik Semoga bermanfaat dengan apa yang dibagikan pelajarancg.blogspot.com!!
Daftar Pustaka:
Herrhyanto, Nar dan H.M. Akib Hamid. 2007. Statistika Dasar. Jakarta: Universitas Terbuka
Richard A. Johnson dan Gouri K. Bhattacharya. 2010. Statistics Principles & Methods. United States of America: John Wiley & Sons, Inc
Statistika. https://id.m.wikipedia.org/wiki/Statistika. diakses: 16 juli 2019