Hai Sobat, kali ini kita akan membicarakan ihwal Momen Inersia
Dalam pelajaran fisika mulai dari SMP sampai Universitas pasti akan memperoleh dilema yang bekerjasama dengan momen inersia.
Sebenarnya apa itu momen inersia?
Moment inersia itu merupakan suatu ilmu fisika yang mempelajari wacana seberapa besar kekuatan untuk menggerakan benda yang berupa batang, silinder, bola, dan sebagainya pada sebuah poros.
Materi ini sedikit buku yang menerangkan persamaan turunan secara lengkap oleh sebab itu bahan ini menarik untuk kita diskusikan Bersama. Simak terus ya…
Daftar Isi
Materi Momen Inersia
Hukum Newton 1 menyampaikan “Benda yang bergerak akan cenderung tetap bergeraksedangkan benda yang diam akan cenderung membisu”.
Secara matematis dapat ditulis ∑F=0 atau dv/dt=0.
Inersia ialah kecenderungan benda untuk mempertahankan keadaannya (tetap membisu atau bergerak).
Inersia juga lazimdisebut dengan kelembaman suatu benda. Oleh karena itu Hukum Inersia juga disebut Hukum Kelembaman.
Besar momen inersia mampu dipengaruhi oleh beberapa faktor, antara lain :
- Massa benda
- Bentuk benda
- Letak sumbu putar
- Jarak dari sumbu putar
Baca Juga: Momen Gaya
Jenis Momen Inersia
1. Momen Inersia Partikel
Momen inersia partikel merupakan momen inersia yang melihat suatu benda sebagai partikel yang sangat kecil.
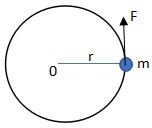
Rumus Momen Inersia Partikel
I=mr2
2. Momen Inersia Benda Tegar
Momen inersia ini menganggap partikel tersebar menyeluruh di setiap bab benda. Setiap partikel itu punya era dan tentu saja memiliki jarak r dari suatu porosnya.
Rumus Momen Inersia Benda Tegar
I=∑mr2
- Batang silinder (poros tengah)
I=1/12mr2
- Batang silinder (poros ujunga)
I=1/3mr2
- Bola Pejal
I=2/5mr2
- BolaBerongga
I=2/3mr2
Keterangan:
- I = momen inersia
- m = massa benda
- r = panjang benda
Momen Inersia dalam Kehidupan Sehari Hari
Momen Inersia banyak dipraktekkan dalam kehidupan sehari hari mulai dari sektor pertanian, farmasi, pendidikan, serta mesin industri.
Sektor Farmasi
Pertama kita akan membahas dalam sektor farmasi. Sentrifugasi dalam melakukan pemisahan adonan materi kimia.
Mesin sentrifugasi memanfaatkan momen inersia dari kesetimbangan antara tabung sentrifugasi untuk memisahkan adonan materi kimia, alasannya adalah jika tidak setimbang, maka akan terjadi sesuatu yang tidak diinginkan seperti getaran berlebih pada mesin yang bisa berakibat pada pecahnya tabung yang lain.
Sektor Mesin Industri
Selanjutnya kita akan sektor mesin industri. Pada mesin bubut kita juga menerapkan rancangan ini, dimana mesin bubut ialah mesin yang digunakan untuk membuat barang dari logam.
Cara kerja mesin bubut ialah memutarkan mata roda selaku pencetaknya.
Jika kita tidak mengamati momen inersia yang ada pada mata roda mesin bubut tersebut maka hasil cetakannya akan tidak karuan bahkan mampu menjadikan kecelakaan yang fatal.
Selanjutnya kita akan membicarakan acuan soal dan cara menyelesaikan dilema Momen Inersia.
Contoh Soal Momen Inersia
1. Bola bermassa 100 gram dihubungkan dengan seutas tali yang panjangnya 30 cm seperti pada gambar. Momen inersia bola terhadap sumbu AB adalah…
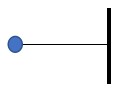
Diketahui:
m = 100 gr = 0.1 kg
r = 30 cm = 0.3 m
Jawab :
I = mr2
I = 0.1 x 0.32
I = 0.0009 kg m2
Makara, Momen inersia bola kepada sumbu AB ialah 0.0009 kg m2
2. Massa masing-masing bola yakni 100 gram, dihubungkan dengan kawat yang massanya diabaikan. Panjang kawat yakni 60 cm dan lebar kawat ialah 30 cm. Tentukan momen inersia tata cara bola terhadap sumbu AB…
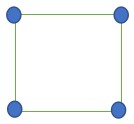
Diketahui :
Massa bola 1 (m1) = m2 = m3 = m4 = 100 gram = 100/1000 = 0,1 kilogram
Jarak bola 1 dari sumbu rotasi (r1) = 30 cm = 30/100 = 0,3 meter
Jarak bola 2 dari sumbu rotasi (r2) = 30 cm = 30/100 = 0,3 meter
Jarak bola 3 dari sumbu rotasi (r3) = 30 cm = 30/100 = 0,3 meter
Jarak bola 4 dari sumbu rotasi (r4) = 30 cm = 30/100 = 0,3 meter
Jawab :
I = m1 r12 + m2 r22 + m3 r32 + m4 r42
I = (0,1 kg)(0,3 m)2 + (0,1 kg)(0,3 m)2 + (0,1 kg)(0,3 m)2 + (0,1 kg)(0,3 m)2
I = (0,1 kg)(0,09 m2) + (0,1 kg)(0,09 m2) + (0,1 kg)(0,09 m2) + (0,1 kg)(0,09 m2)
I = 0,036 kg m2
Jadi, momen inersia sistem bola kepada sumbu AB yaitu 0,036 kg m2
3. Suatu bola kasti bermassa 80 gram diikat memakai tali sepanjang 20 cm mirip pada gambar.
Momen inersia bola tersebut kepada sumbu XY adalah…
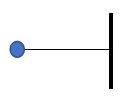
Sumbu rotasi adalah XY
Massa bola (m) = 80 g = 0,08 kg
Jarak bola dari sumbu rotasi (r) = 20 cm = 0,2 m
Penyelesaian :
I = m r 2
I = (0,08 kg) × (0,2 m)2
I = (0,08 kg) × (0,04 m2)
I = 0,0032 kg m2
Makara, Momen inersia bola tersebut terhadap sumbu XY yakni 0,0032 kg m2.
4. Diketahui 2 bola masing-masing mempunyai massa 200 gram dan 400 gram. Kedua bola terhubung dengan suatu kawat sepanjang 50 cm yang massanya diabaikan. Sumbu XY terletak di tengah kawat. Berapakah momen inersia tata cara kedua bola tersebut terhadap sumbu XY ?
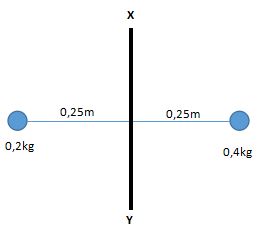
Massa bola 1 (m1) = 200 g = 0,2 kg
Massa bola 2 (m2) = 400 g = 0,4 kg
Jarak bola 1 dari sumbu rotasi (r1) = Jarak bola 2 dari sumbu rotasi (r2) = 25 cm = 0,25 m
Penyelesaian
I = m1 r12 + m2 r22
I = (0,2 kg)(0,25 m)2 + (0,4 kg)(0,25 m)2
I = (0,2 kg)(0,0625 m2) + (0,4 kg)(0,0625 m2)
I = 0,0125 kg m2 + 0,025 kg m2
I = 0,0375 kg m2
Makara, momen inersia metode kedua bola tersebut kepada sumbu XY adalah 0,0375 kg m2.
5. Diketahui 2 bola masing-masing memiliki massa 300 gram dan 100 gram. Kedua bola terhubung dengan sebuah kawat sepanjang 40 cm yang massanya diabaikan. Sumbu XY terletak di bola bermassa 100 gram. Berapakah momen inersia metode kedua bola tersebut kepada sumbu XY ?
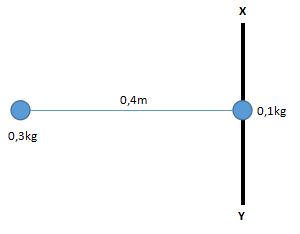
Massa bola 1 (m1) = 300 g = 0,3 kg
Massa bola 2 (m2) = 100 g = 0,1 kg
Jarak bola 1 dari sumbu rotasi (r1) = 40 cm = 0,4 m
Jarak bola 2 dari sumbu rotasi (r2) = 0 meter
Penyelesaian
I = m1 r12 + m2 r22< /p>
I = (0,3 kg)(0,4 m)2 + (0,1 kg)(0 m)2
I = (0,2 kg)(0,16 m2) + 0
I = 0,032 kg m2
Makara, momen inersia metode kedua bola tersebut kepada sumbu XY yakni 0,032 kg m2.
6. Diketahui 4 bola bermassa sama adalah yakni 200 gram, dihubungkan menggunakan kawat yang massanya diabaikan. Panjang kawat adalah 80 cm dan lebar kawat yaitu 40 cm. Jika sumbu XY berada di tengah-tengah panjang kawat, hitunglah momen inersia metode bola kepada sumbu XY.
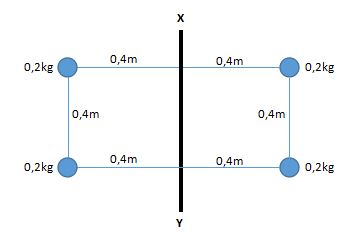
Massa bola: m1 = m2 = m3 = m4 = 200 g = 0,2 kg
Jarak bola dari sumbu rotasi: r1 = r2 = r3 = r4 = 80 cm = 0,4 m
Penyelesaian:
I = m1 r12 + m2 r22 + m3 r32 + m3 r32
I = 4 m1 r12
I = 4 (0,2 kg)(0,4 m)2
I = 4 (0,2 kg)(0,16 m2)
I = 0,128 kg m2
Jadi, momen inersia metode bola terhadap sumbu XY yaitu 0,128 kg m2.
7. Sebuah tongkat bermassa 3 kg dan panjang yakni 4 meter. Berapakah momen inersia tongkat jikalau sumbu rotasi terletak di tengah batang!
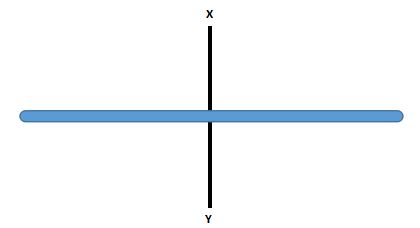
Massa batang pejal (M) = 3 kg
Panjang batang pejal (L) = 4 meter
Rumus momen inersia batang untuk sumbu rotasi di tengah batang :
I = (1/12) M L2
I = (1/12) (3 kg)(4 m)2
I = (1/12) (3 kg)(16 m2)
I = (1/12)(48 kg m2)
I = 4 kg m2
Makara, momen inersia tongkat kalau sumbu rotasi terletak di tengah batang adalah 4 kg m2.
8. Sebuah tongkat bermassa 3 kg dan panjang yakni 4 meter. Berapakah momen inersia tongkat bila sumbu rotasi terletak di salah satu ujung batang ?

Massa batang pejal (M) = 3 kg
Panjang batang pejal (L) = 4 meter
Rumus momen inersia batang untuk sumbu rotasi di salah satu ujung batang :
I = (1/3) M L2
I = (1/3) (3 kg)(4 m)2
I = (1/3) (3 kg)(16 m2)
I = 16 kg m2
Jadi, momen inersia tongkat jika sumbu rotasi terletak di salah satu ujung batang yaitu 16 kg m2.
9. Hitunglah momen inersia cakram pejal (padat) bermassa 20 kg dan berjari-jari 0,2 meter, jikalau sumbu rotasi ada di pusat cakram!
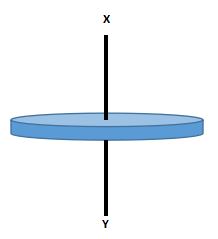
Massa cakram pejal (M) = 20 kg
Jari-jari cakram pejal (L) = 0,2 meter
Momen inersia batang kalau sumbu rotasi terletak di sentra cakram yaitu :
I = ½ M L2
I = ½ (20 kg)(0,2 m)2
I = ½ (20 kg)(0,04 m2)
I = ½ (0,8 kg m2)
I = 0,4 kg m2
Jadi, momen inersia cakram pejal tersebut ialah 0,4 kg m2.
Demikian pembahasan perihal Momen Inersia
Semoga bermanfaat
Jangan lupa tersenyum 😀