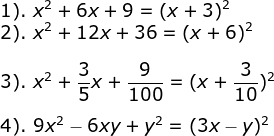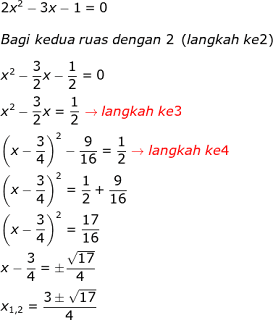Melengkapkan Kuadrat Sempurna Desain Dan Contoh Soal Persamaan Kuadrat

by

[]).push();

 

 

Sebelumnya kalian niscaya telah mengenal persamaan kuadrat dengan bentuk biasa            ax2 +bx+ c =0 ada beberapa cara memilih himpunan penyelesaian persamaan kuadrat yakni dengan pemfaktoran , dengan rumus abc dan dengan melengkapkan kuadrat sempurna.

Apa yang dimaksud dengan melengkapkan kuadrat tepat?


Cara melengkapkan kuadrat sempurna atau bentuk kuadrat sempurna yaitu bentuk persamaan kuadrat yang dapat di nyatakan kedalam bentuk  (a+b)2. Contoh persamaan kuadrat yang berupa kuadrat sempurna:






Pada pembahasan kali ini akan fokus pada cara yang terakhir saja yakni melengkapkan kuadrat sempurna. Ada persamaan kuadrat yang tidak bisa di tentukan himpunan solusi atau nilai akar-akarnya dengan cara pemfaktoran atau dengan rumus abc, persamaan kuadrat seperti ini bisa di pastikan himpunan solusi atau nilai akar-akarnya dengan cara melengkapkan kuadrat tepat.


Agar lebih mudah di ketahui pada pembahasan ini menyelesaikan persamaaan kuadrat dengan melengkapkan kuadrat tepat di bagi menjadi dua yakni bentuk persamaan kuadrat    ax2 +bx+ c =0 jika a = 1 dan bentuk ax2 +bx+ c =0 jikalau a≠ 1. 

Tentunya sudah paham ya mana koofisien x2 ? mana koofisien x ? dan yang mana konstanta? Jika belum silahkan pelajari di bagian lain blog ini.

Langkah-langkah melengkapkan kuadrat tepat:

  1. Pastikan koefisien x2 = 1
  2. Jika koefisien x2 ≠ 1,  bagilah  persamaan kuadrat dengan koofisien x2  
  3. Pindahkan konstanta c ke ruas kanan
  4. Koofisien x di bagi dengan 2 kemudian di kurang (b/2)2 
  5. Selesaikan persamaan kuadrat untuk menentukan akar-akarnya


Contoh soal dan Penyelesaian persamaan kuadrat dengan cara melengkapkan kuadrat tepat

Untuk menuntaskan soal-soal di bawah ini senantiasa gunakan tindakan melengkapkan kuadrat sempurna di atas.

  Melengkapkan Kuadrat Tepat Konsep Dan Pola Soal Persamaan Kuadrat

Tentukan Himpunan solusi setiap persamaan kuadrat di bawah ini!

Contoh 1


Pada teladan 1 ini koofisien x2 = 1 , jadi pribadi ke langkah ke tiga.


Contoh 2

Masih sama seperti teladan 1 dimana koofisien x2 = 1, jadi langsung ke langkah ke tiga







Contoh 3

Tentukan akar-akar persamaan kuadrat berikut dengan melengkapkan kuadrat tepat!



















Contoh 4:


Tentukan akar-akar persamaan kuadrat berikut dengan melengkapkan kuadrat sempurna!










Untuk contoh 5 dan seterusnya pembahasan soal fokus pada bentuk persamaan kuadrat ax2 +bx+ c =0 kalau a≠ 1.

Contoh 5

Tentukan akar-akar persamaan kuadrat berikut dengan melengkapkan kuadrat tepat!

Contoh 6
Tentukan akar-akar persamaan kuadrat berikut dengan melengkapkan kuadrat tepat!


















Contoh 7

Selesaikan persamaan kuadrat berikut dengan melengkapkan kuadrat tepat!

Praktis-mudahan bisa di ketahui penjelasan Konsep dan acuan soal  persamaan kuadrat dengan melengkapkan kuadrat tepat di atas, supaya berguna.