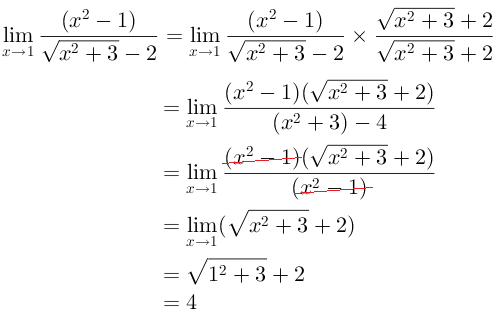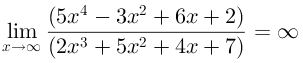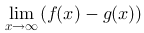Limit Fungsi Aljabar Matematika SMA & SMK
Limit fungsi aljabar – Limit fungsi adalah suatu nilai pendekatan disekitar titik tertentu baik pendekatan dari kiri suatu titik maupun pendekatan dari kanan titik tersebut (Dedi Heryadi, 2007). Secara umum didefinisikan sebagai berikut:
lim x mendekati n f(x) = A, jika dan hanya jika x mendekati n , x≠ n maka maka f(x) mendekati nilai A.
Cara menghitung Limit Fungsi aljabar
Ada beberapa cara untuk menghitung nilai limit fungsi aljabar, yaitu:
- Dengan subtitusi langsung
- Mengalikan dengan akar sekawan atau faktor lawan
- Membagi dengan pangkat tertinggi
Kelima teknik menghitung nilai limit fungsi aljabar diatas didasarkan pada “kondisi tertentu”, artinya teknik mana yang paling mudah dan tepat untuk digunakan bergantung pada kondisi soalnya . Oleh karena itu perlu analisa dan pemahaman yang baik dalam menggunakan kelima cara diatas, berikut ini akan dibahas satu-persatu teknik atau metode tersebut.
Menghitung Nilai Limit fungsi aljabar dengan substitusi langsung
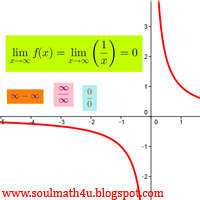
Menghitung nilai limit fungsi dengan subtitusi langsung dapat dilakukan dengan syarat pada perhitungan dengan subtitusi langsung tidak diperoleh bentuk tak tentu seperti 0/0, ∞ /∞ , ∞ -∞ bentuk-bentuk seperti ini disebut bentuk tak tentu. Jika dengan subtitusi langsung diperoleh bentu tak tentu maka penghitungan nilai limit fungsi aljabar menggunakan cara lain.
Contoh soal menghitung limit fungsi aljabar dengan subtitusi langsung
Hitunglah nilai limit setiap fungsi berikut:
Menghitung limit fungsi aljabar dengan cara pemfaktoran atau faktorisasi
Jika dengan cara subtitusi langsung diperoleh bentuk tak tentu 0/0 atau
maka perhitungan nilai limit dilakukan dengan cara memfaktorkan jika belum paham pelajari dahulu ya, materi pemfaktoran. Perhatikan contoh-contoh berikut ini,
Hitunglah nilai limit fungsi aljabar berikut ini:
Dengan subtitusi langsung akan diperoleh ,
diperoleh bentuk tak tentu maka dilakukan dengan cara memfaktorkan,
Limit fungsi aljabar bentuk akar
Dalam menghitung nilai limit fungsi aljabar terkadang kita jumpai bentuk akar, maka cara menyelesaikannya adalah dengan mengalikan akar sekawan . Perhatikan contoh-contoh soal berikut ini,
Hitunglah nilai limit fungsi dibawah ini:
Dengan subtitusi langsung ,
diperoleh bentuk tak tentu, maka harus menggunakan cara lain yaitu mengalikan dengan akar sekawan.
Supaya lebih jelas perhatikan kembali soal No 2 berikut ini,
Subtitusi langsung akan menghasilkan 0/0, maka:
Limit Fungsi Bentuk Tak Tentu Untuk x Mendekati Tak berhingga
Dalam bahasa matematika untuk menyatakan suatu keadaan atau kondisi yang nilai dan besarnya tidak dapat ditentukan digunakan lambang ∞ (dibacanya tak berhingga). Soal-soal limit fungsi aljabar dengan variabel atau peubah x mendekati tak berhingga, biasanya sering dijumpai dalam bentuk umum seperti dibawah ini:
Bentuk umum limit fungsi aljabar x mendekati tak berhingga adalah,
Jika menggunakan metode subtitusi langsung akan diperoleh bentuk tak tentu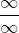 
atau ∞ – ∞. Maka cara menghitung nilai limit fungsi aljabar untuk x mendekati tak berhingga menggunakan cara-cara sebagai berikut:
-
Membagi dengan pangkat tertinggi
-
Mengalikan dengan sekawan atau faktor lawan
Nah, sekarang kita bahas satu persatu ya…
Limit fungsi Aljabar – Membagi dengan pangkat tertinggi
Menghitung nilai lim x → ∞ f(x)/g(x) dapat dilakukan dengan cara membagi pembilang f(x) dan penyebut g(x) dengan x^n, dengan n adalah pangkat tertinggi dari f(x) ataupun g(x). Tapi sebelumnya catat terlebih dahulu rumus dibawah ini :
Hitunglah nilai limit fungsi aljabar berikut ini!
[Penyelesaian]
Perhatikan f(x) dan g(x) mempunyai pangkat tertinggi yaitu 1, maka pembilang dan penyebut masing-masing dibagi x, maka
Perhatikan f(x) dan g(x) mempunyai pangkat tertinggi yaitu 3, maka pembilang dan penyebut masing-masing dibagi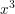 
, maka
Perhatikan kembali contoh No 3 dibawah ini:
[Penyelesaian]
Perhatikan f(x) dan g(x) mempunyai pangkat tertinggi yaitu 4, maka pembilang dan penyebut masing-masing dibagi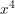 
, maka
Dari contoh-contoh diatas ada rumus cepat menghitung nilai limit fungsi aljabar bentuk
, yaitu:
1.Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x)
2. Jika pangkat tertinggi f(x) > pangkat tertinggi g(x)
3. Jika pangkat tertinggi f(x) < pangkat tertinggi g(x)
Sekarang rumus-rumus diatas akan dipakai untuk menyelesaikan contoh soal limit fungsi aljabar berikut ini,
Hitunglah nilai setiap limit fungsi dibawah ini!
[Penyelesaian]
Dari soal diatas, pangkat tertinggi f(x) = pangkat tertinggi g(x) yaitu pangkat 3 maka memenuhi (1) jadi
Contoh No 2 ini jika pangkat tertinggi f(x) > pangkat tertinggi g(x):
Dari soal diatas, pangkat tertinggi f(x) > pangkat tertinggi g(x) memenuhi (2) jadi
Kalau soal No 3 ini pangkat tertinggi f(x) < pangkat tertinggi g(x)
Dari soal diatas, pangkat tertinggi f(x) < pangkat tertinggi g(x) memenuhi (3) jadi
Limit fungsi Aljabar – Mengalikan dengan faktor lawan/ sekawan
Cara mengalikan dengan faktor lawan biasanya limit fungsi aljabar nya berbentuk
Agar lebih jelas perhatikan contoh soal dibawah ini!
Hitunglah nilai limit fungsi berikut:
[Penyelesaian]
Selain cara menggunakan cara mengalikan dengan faktor lawan atau kalikan sekawan ada atau cara lain menghitung nilai limit fungsi aljabar bentuk lim x → ∞ √ f(x)- √ g(x)} yaitu dengan syarat f(x) dan g(x) merupakan fungsi kuadrat , rumus nya adalah :
Rumus cepat :
Perhatikan contoh dibawah ini !
b = -2 ; d = 3 dan a = 4 , Gunakan rumus cepat diatas!
Relatif mudah bukan? yang terpenting adalah kalian harus dapat menerapkan cara-cara dan teknik yang tepat dalam menghitung limit fungsi aljabar.
