Sistem persamaan linear dua variabel (peubah) atau disingkat SPLDV ialah suatu persamaan matematika yang terdiri atas dua persamaan linear yang masing-masing bervariabel dua (misal x dan y). Dengan demikian, bentuk biasa SPLDV ialah sebagai berikut.
ax + by = c ……………….. Persamaan (1)
px + qy = r ……………….. Persamaan (2)
px + qy = r ……………….. Persamaan (2)
dengan a, b, c, p, q, dan r merupakan bilangan real.
Nah, pada kesempatan kali ini kita akan menyajikan kumpulan teladan soal dan pembahasan tentang tata cara persamaan linear dua variabel (SPLDV) dengan memakai berbagai macam sistem. Silahkan disimak baik-baik.
Contoh Soal Sistem Persamaan Linear Dua Variabel (SPLDV)
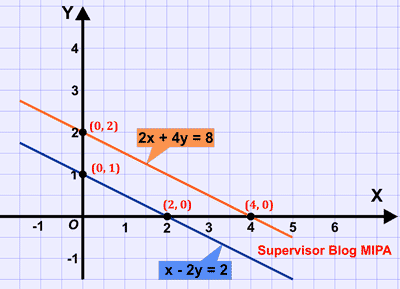
1. Tentukan himpunan solusi dari sistem persamaan x + 2y = 2 dan 2x + 4y = 8 untuk x, y ∈ R menggunakan sistem grafik.
Penyelesaian
Pertama, kita tentukan titik potong masing-masing persamaan pada sumbu-X dan sumbu-Y
■ x + 2y = 2
Titik potong dengan sumbu-X, syaratnya ialah y = 0
⇔ x + 2(0) = 2
⇔ x = 2
Titik potong (2, 0)
Titik potong dengan sumbu-Y, syaratnya adalah x = 0
⇔ 0 + 2y = 2
⇔ 2y = 2
⇔ y = 1
Titik potong (0, 1)
■ 2x + 4y = 8
Titik potong dengan sumbu-X, syaratnya yaitu y = 0
⇔ 2x + 4(0) = 8
⇔ 2x = 8
⇔ x = 4
Titik potong (4, 0)
Titik potong dengan sumbu-Y, syaratnya yakni x = 0
⇔ 2(0) + 4y = 8
⇔ 4y = 8
⇔ y = 2
Titik potong (0, 2)
Kedua, kita gambarkan grafik dari masing-masing persamaan pada sebuah bidang Cartesius seperti yang ditunjukkan pada gambar di bawah ini.
Berdasarkan gambar grafik metode persamaan di atas, terlihat bahwa kedua garis tersebut tidak akan pernah berpotongan alasannya adalah keduanya sejajar. Dengan demikian, himpunan solusi dari sistem persamaan x + 2y = 2 dan 2x + 4y = 8 adalah himpunan kosong, ditulis atau ∅.
2. Dengan menggunakan tata cara subtitusi, tentukanlah himpunan penyelesaian dari SPLDV berikut ini.
2x – 3y = 7
3x + 2y = 4
Jawab
2x – 3y = 7 ………. Pers. (7)
3x + 2y = 4 ………. Pers. (8)
Dari persamaan (7) kita dapatkan persamaan x selaku berikut.
|
⇔
|
2x – 3y
|
=
|
7
|
|
⇔
|
2x
|
=
|
7 + 3y
|
|
⇔
|
x
|
=
|
7 + 3y
|
|
2
|
Subtitusikan persamaan x ke dalam persamaan (8) selaku berikut.
|
⇔
|
3
|
(
|
7 + 3y
|
)
|
+
|
2y
|
=
|
4
|
|
2
|
||||||||
|
⇔
|
3(7 + 3y) + 4y
|
=
|
8 (kedua ruas dikali 2)
|
|||||
|
⇔
|
21 + 9y + 4y
|
=
|
8
|
|||||
|
⇔
|
21 + 13y
|
=
|
8
|
|||||
|
⇔
|
13y
|
=
|
8 – 21
|
|||||
|
⇔
|
13y
|
=
|
-13
|
|||||
|
⇔
|
y
|
=
|
-1
|
|||||
Untuk memilih nilai x, kita subtitusikan nilai y ke persamaan (7) atau persamaan (8) sebagai berikut.
⇔ 2x – 3(-1) = 7
⇔ 2x + 3 = 7
⇔ 2x = 7 – 3
⇔ 2x = 4
⇔ x = 2
Dengan demikian, himpunan penyelesaian dari SPLDV tersebut yaitu (2, -1).
3. Dengan menggunakan tata cara eliminasi, carilah himpunan solusi dari persamaan berikut ini.
|
x – 2
|
+
|
y
|
=
|
3
|
|
4
|
|
x
|
+
|
y + 4
|
=
|
8
|
|
3
|
Jawab
Kedua bentuk SPLDV di atas belum baku, alasannya itu, perlu diubah apalagi dahulu menjadi bentuk baku. Caranya ialah persamaan pertama kita kalikan 4 pada kedua ruasnya sedangkan persamaan kedua kita kalian 3 pada kedua ruasnya, sehingga menciptakan persamaan berikut ini.
Persamaan pertama:
x – 2 + 4y = 12
x + 4y = 12 + 2
x + 4y = 14
Persamaan kedua:
3x + y + 4 = 24
3x + y = 24 – 4
3x + y = 20
Dengan demikian, tata cara persamaan semula ekuivalen dengan SPLDV berikut ini.
x + 4y = 14
3x + y = 20
Selanjutnya, SPLDV yang terakhir ini mampu terselesaikan dengan menggunakan sistem eliminasi yakni selaku berikut:
Untuk mengeliminasi x, maka kalikan persamaan pertama dengan 3 agar koefisien x kedua persamaan sama. Selanjutnya kita selisihkan kedua persamaan sehingga kita peroleh nilai y sebagai berikut.