Implikasi merupakan kalimat majemuk dengan tanda hubung “kalau … maka …” dan ditulis “⇒”. Untuk memilih nilai tabel kebenarannya, amati citra berikut. Misalkan jika Lia lulus cobaan maka ia akan menawarkan duit kepada adiknya.
Misalnya:
p: Lia lulus cobaan.
q: Lia memberikan uang terhadap adiknya.
kini kita pastikan negasi dari p dan q selaku berikut.
p: Lia tidak lulus ujian.
q: Lia tidak menawarkan duit terhadap adiknya.
Dari pernyataan di atas, kita mampu membuat hubungan implikasi selaku berikut.
1. Jika Lia lulus cobaan maka beliau akan memperlihatkan duit terhadap adiknya.
(kalimat ini bernilai benar karena Lia menepati janji)
2. Jika Lia lulus ujian maka ia tidak menunjukkan uang kepada adiknya.
(kalimat ini salah alasannya Lia tidak menepati kesepakatan)
3. Jika Lia tidak lulus ujian maka ia menawarkan uang kepada adiknya.
(kalimat ini bernilai benar alasannya meskipun janjinya gugur dia tetap menawarkan duit kepada adiknya)
4. Jika Lia tidak lulus cobaan maka beliau tidak menunjukkan duit kepada adiknya.
(kalimat ini bernilai benar karena Lia bebas dari janjinya)
Dari citra di atas, kita dapat menyusun nilai tabel kebenaran implikasi sebagai berikut.
Tabel Nilai Kebenaran Implikasi
|
p
|
q
|
p ⇒ q
|
|
B
|
B
|
B
|
|
B
|
S
|
S
|
|
S
|
B
|
B
|
|
S
|
S
|
B
|
Contoh Soal 1:
Tentukan nilai kebenaran dari implikasi dua pernyataan berikut.
p: Pak Rudi yaitu manusia. (benar)
q: Pak Rudi kelak akan mati. (benar)
Jawab:
p ⇒ q: Jika Pak Rudi adalah manusia, maka kelak akan mati. (benar)
Contoh Soal 2:
Tentukan nilai kebenaran dari implikasi dua pernyataan berikut.
p: 2 + 5 = 7 (benar)
q: 7 bukan bilangan prima (salah)
Jawab:
p ⇒ q: Jika 2 + 5 = 7, maka 7 bukan bilangan prima (salah).
Contoh Soal 3:
Carilah nilai-nilai x supaya setiap kalimat berikut ini menjadi implikasi yang bernilai benar.
a) Jika x < 2 maka 2log 4 = 1/2
b) Jika 31/2 = √3 maka 1 – 2x = x – 8
Penyelesaian:
a) terdapat suatu kalimat terbuka yakni p(x): x < 2 dan pernyataan q: 2log 4 = 1/2. Nilai kebenaran pernyataan q kita tentukan sebagai berikut.
2log 4 = 2log 22 = 2
Dengan demikian, pernyataan q bernilai salah (S). Agar p ⇒ q menjadi implikasi yang benar maka kalimat terbuka p(x) harus bernilai salah. Nilai x yang menyanggupi yakni selaku berikut.
x < 2, maka x harus lebih besar dari atau sama dengan 2 untuk x ∈ R.
Kaprikornus, supaya kalimat “Jika x < 2 maka 2log 4 = 1/2” menjadi implikasi yang benar, maka nilai x ≥ 2, untuk x ∈ R.
b) Terdapat suatu pernyataan p: 31/2 = √3 dan kalimat terbuka q(x): 1 – 2x = x – 8. Nilai kebenaran pernyataan p kita pastikan selaku berikut.
31/2 = 2√31 atau cuma ditulis selaku √3
Dengan demikian, pernyataan p bernilai benar (B). Agar p ⇒ q menjadi implikasi yang benar maka kalimat terbuka q(x) mesti menjadi pernyataan yang bernilai benar, sehingga nilai x yang memnuhi yakni sebagai berikut.
1 – 2x = x – 8
x + 2x = 1 + 8
3x = 9
x = 9/3
x = 3
Jadi, semoga kalimat “Jika 31/2 = √3 maka 1 – 2x = x – 8” menjadi implikasi yang benar, maka nilai x yang memenuhi yaitu 3.
Contoh Soal 4:
Carilah nilai-nilai x semoga setiap kalimat berikut ini menjadi implikasi yang bernilai salah.
a) Jika x2 – 1 = 0 maka sin2 45o = 1.
b) Jika √2 + √8 = 3√2 maka x – 2 ≠ 1.
Penyelesaian:
a) Terdapat suatu kalimat terbuka p(x): x2 – 1 = 0 dan pernyataan q: sin2 45o = 1. Nilai kebenaran pernyataan q kita pastikan selaku berikut.
sin2 45o = (sin 45)2
sin2 45o = (1/2√2)2
sin2 45o = 1/4(2)
sin2 45o = 2/4
sin2 45o = 1/2
Dengan demikian, pernyataan q bernilai salah (S). Agar p ⇒ q menjadi implikasi yang bernilai salah, maka kalimat terbuka p(x) mesti menjadi pernyataan yang bernilai benar, sehingga nilai x yang menyanggupi yakni selaku berikut.
x2 – 1 = 0
(x – 1)(x + 1) = 0
x = 1 atau x = -1
Makara, supaya kalimat “Jika x2 – 1 = 0 maka sin2 45o = 1” menjadi implikasi yang salah, maka nilai x yaitu 1 atau -1.
b) Terdapat sebuah pernyataan p: √2 + √8 = 3√2 dan kalimat terbuka q(x): x – 2 ≠ 1. Nilai kebenaran pernyataan p yakni selaku berikut.
√2 + √8 = √2 + √(4 × 2)
√2 + √8 = √2 + √4 × √2
√2 + √8 = √2 + 2 × √2
√2 + √8 = √2 + 2√2
√2 + √8 = 3√2
Dengan demikian, pernyataan p bernilai benar (B). Agar p ⇒ q menjadi implikasi yang bernilai salah, maka kalimat terbuka q(x) harus menjadi pernyataan yang bernilai salah, sehingga nilai x yang memenuhi adalah sebagai berikut.
x – 2 = 1
x = 1 + 2
x = 3
jikalau nilai x = 3, maka kalimat terbuka x – 2 ≠ 1 akan menjadi pernyataan yang bernilai salah (S).
Makara, semoga kalimat “Jika √2 + √8 = 3√2 maka x – 2 ≠ 1” menjadi implikasi yang bernilai salah, maka nilai x adalah 3.
Hubungan antara Implikasi dengan Himpunan Bagian
|
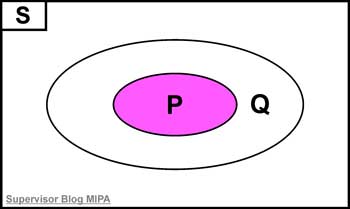
Jika P dan Q masing-masing merupakan himpunan penyelesaian dari kalimat terbuka p(x) dan q(x) pada himpunan semesta S, maka p ⇒ q benar jikalau P ⊂ Q.
|
Atau dalam bentuk lambang himpunan mampu dituliskan sebagai berikut.
P = p(x), p benar jika x ∈ P
Q = q(x), Q benar jikalau x ∈ Q
Implikasi p ⇒ q benar, kalau P ⊂ Q
Hubungan tersebut mampu digambarkan dengan diagram Venn seperti yang ditunjukkan pada gambar berikut ini.
Contoh Soal 5:
Dalam semesta obrolan S = 0, 1, 2, 3, 4, 5, 6, tentukan nilai kebenaran setiap implikasi berikut ini.
a) Jika 1 ≤ x ≤ 2 maka x2 – 5x + 4 ≤ 0
b) Jika x2 – 5x + 4 ≤ 0 maka 1 ≤ x ≤ 2
Jawab:
Misalkan:
P yakni himpunan penyelesaian kalimat terbuka p(x): 1 ≤ x ≤ 2 dalam semesta obrolan S, maka P = 1, 2.
Q yaitu himpunan solusi kalimat terbuka q(x): x2 – 5x + 4 ≤ 0 dalam semesta pembicaraan S, maka Q = 1, 2, 3, 4.
Hubungan antara P dan Q diperlihatkan dengan diagram Venn pada gambar di bawah ini.
Dari gambar di atas, tampak bahwa P ⊂ Q tetapi Q ⊂ P. Dengan demikian:
a) p(x) ⇒ q(x) bernilai benar, atau bila 1 ≤ x ≤ 2 maka x2 – 5x + 4 ≤ 0, ialah implikasi yang benar.
b) q(x) ⇒ p(x) bernilai salah, atau jikalau x2 – 5x + 4 ≤ 0 maka 1 ≤ x ≤ 2, ialah implikasi yang salah.