Kalian sudah mengenal kalimat beragam implikasi. Dari tabel nilai kebenaran implikasi itu, coba kalian perhatikan tabel nilai kebenaran berikut ini.
|
p
|
q
|
p ⇒ q
|
q ⇒ p
|
(p ⇒ q) ∧ (q ⇒ p)
|
|
B
|
B
|
B
|
B
|
B
|
|
B
|
S
|
S
|
B
|
S
|
|
S
|
B
|
B
|
S
|
S
|
|
S
|
S
|
B
|
B
|
B
|
Dari tabel di atas, nilai kebenaran dari (p ⇒ q) ∧ (q ⇒ p) yakni nilai kebenaran biimplikasi. Biimpilkasi yakni dua kalimat pernyataan yang memakai kata hubung “jikalau dan cuma jikalau” dan dilambangkan dengan “⇔”. Oleh alasannya adalah itu, (p ⇒ q) ∧ (q ⇒ p) ≡ p ⇔ q. Tanda “≡” adalah tanda ekuivalen.
Kaprikornus, dapat kita simpulkan bahwa nilai kebenaran dari sebuah pernyataan beragam biimplikasi ditunjukkan mirip pada tabel berikut ini.
Tabel Nilai Kebenaran Biimplikasi
|
p
|
q
|
p ⇔ q
|
|
B
|
B
|
B
|
|
B
|
S
|
S
|
|
S
|
B
|
S
|
|
S
|
S
|
B
|
Contoh Soal 1:
Tentukan nilai kebenaran dari biimplikasi dua pernyataan berikut.
p: 3 × 2 = 6 (benar)
q: 6 memiliki faktor 1, 2, 3, 4, 6 (salah)
Jawab:
p ⇔ q: 3 × 2 = 6 kalau dan cuma bila 6 memiliki faktor 1, 2, 3, 4, 6. (salah)
Contoh Soal 2:
Tentukan nilai kebenaran dari biimplikasi dua pernyataan berikut.
p: Persegi mempunyai 5 simetri lipat. (salah)
q: Persegi memiliki 2 simetri putar. (salah)
Jawab:
p ⇔ q: Persegi memiliki 5 simetri lipat kalau dan cuma bila mempunyai 2 simetri putar. (benar)
Contoh Soal 3:
Tentukan nilai kebenaran setiap biimplikasi berikut ini.
a) log 25 – log 4 = 21 kalau dan hanya jika log 25 + log 4 = 2.
b) a = b jika dan cuma jika a + c = b + c, untuk a, b, c ∈ R.
Jawab:
a) Misalkan p: log 25 – log 4 = log 21 dan q: log 25 + log 4 = 2. Kita pastikan nilai kebenaran pernyataan p dan q selaku berikut.
Nilai kebenaran p:
log 25 – log 4 = log (25/4)
log 25 – log 4 = log 6,25
jadi nilai kebenaran pernyataan p yakni salah (S).
Nilai kebenaran p:
log 25 + log 4 = log (25 × 4)
log 25 + log 4 = log 100
log 25 + log 4 = log 102
log 25 + log 4 = 2
jadi nilai kebenaran pernyataan q yakni benar (B).
alasannya p bernilai salah sedangkan q bernilai benar, maka p ⇔ q salah.
b) Misalkan p: a = b dan q: a + c = b + c. Dengan menggunakan persamaan pada pernyataan p, kita uji nilai kebenaran pernyataan q, adalah sebagai berikut.
a + c = b + c
b + c = b + c
Kaprikornus, pernyataan q benar, sedangkan pernyataan p sudah niscaya benar (saling mensugesti) dengan demikian, p ⇔ q benar.
Contoh Soal 4:
Carilah nilai x supaya kalimat berikut ini menjadi biimplikasi yang bernilai benar.
√9 adalah bilangan irasional jika dan hanya jika x > 2
Jawab:
Terdapat pernyataan p: √9 adalah bilangan irasional dan kalimat terbuka q(x): x > 2. Nilai kebenaran pernyataan p yakni selaku berikut.
√9 = ±3 (bilangan rasional)
Dengan demikian, pernyataan p bernilai salah. Agar p ⇔ q benar, maka kalimat terbuka q(x) harus menjadi pernyataan yang bernilai salah, sehingga nilai x yang memenuhi yakni x ≤ 2, x ∈R.
Contoh Soal 5:
Carilah nilai x agar kalimat berikut menjadi biimplikasi yang bernilai salah.
Log 9 = 2 log 3 kalau dan cuma jikalau x ≥ 5.
Jawab:
Terdapat sebuah pernyataan p: log 9 = 2 log 3 dan kalimat terbuka q(x): x ≥ 5. Nilai kebenaran pernyataan p yakni selaku berikut.
Log 9 = log 32
Log 9 = 2 log 3
Makara, pernyataan p bernilai benar (B). Agar p ⇔ q salah, maka kalimat terbuka q(x) mesti menjadi pernyataan yang bernilai salah sehingga nilai x yang menyanggupi ialah x < 5, x ∈ R.
Hubungan antara Implikasi dengan Himpunan Bagian
|
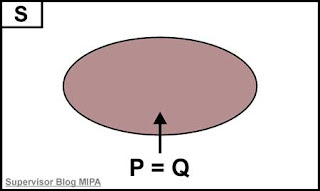
Jika P dan Q masing-masing merupakan himpunan solusi dari kalimat terbuka p(x) dan q(x) pada semesta pembiacaraan S, maka p(x)⇔ q(x) menjadi biimplikasi p ⇔ q yang bernilai benar apabila P = Q.
|
Atau dalam bentuk lambang himpunan dapat dituliskan selaku berikut.
P = p(x), p benar jikalau x ∈ P
Q = q(x), Q benar kalau x ∈ Q
Biimplikasi p ⇔ q benar, bila P = Q
Hubungan tersebut dapat digambarkan dengan diagram Venn seperti yang ditunjukkan pada gambar berikut ini.
Contoh Soal 6:
Di antara pernyataan biimplikasi berikut ini, manakah pernyataan yang mempunyai nilai kebenaran benar (B)?
a) x = 16 jikalau dan hanya jikalau 2log x = 4
b) x – 6 > 0 jika dan cuma jika x2 – 7x + 6 > 0.
c) Dua buah garis sejajar jikalau dan hanya bila garis itu sebidang.
Jawab:
Suatu pernyataan biimplikasi yang berisikan dua kalimat terbuka p(x) dan q(x) akan bernilai benar jika himpunan penyelesaian dari kedua kalimat terbuka tersebut sama.
a) p(x): x = 16 dan q(x): 2log x = 4. Himpunan solusi kedua kalimat terbuka ini yaitu sebagai berikut.
Misalkan himpunan solusi p(x) = P dan q(x): Q maka:
□ x = 16, P = 16
□ 2log x = 4
2log 24 = 4, Q = 24 = 16
Karena P = Q, maka kalimat “x = 16 jika dan cuma bila 2log x = 4” adalah biimplikasi yang benar.
b) p(x): x – 6 > 0 dan q(x): x2 – 7x + 6 > 0. Himpunan penyelesaian kedua kalimat terbuka ini yaitu selaku berikut.
Misalkan himpunan penyelesaian p(x) = P dan q(x): Q maka:
□ x – 6 > 0
x > 6, P = x > 6, x ∈ R.
□ x2 – 7x + 6 > 0
(x – 6)(x – 1) > 0, Q = x
Karena P = Q, maka kalimat “p(x): x – 6 > 0 dan q(x): x2 – 7x + 6 > 0” adalah biimplikasi yang benar.
c) Dua garis sejajar telah niscaya sebidang. Tapi dua garis sebidang, belum pasti sejajar (mampu saja berhimpit). Makara, kalimat “Dua buah garis sejajar kalau dan hanya jika garis itu sebidang” adalah biimplikasi yang benar.