Jenis-Jenis Bilangan Bagian

Pelajarancg: Dalam Mapel matematika, ada tiga jenis utama bagian. Yaitu penggalan murni, pecahan tak murni, dan cuilan adonan. Pecahan adalah suku-suku yang memiliki pembilang dan penyebut. Berdasarkan dua perumpamaan ini kita akan mendefinisikan jenisnya.

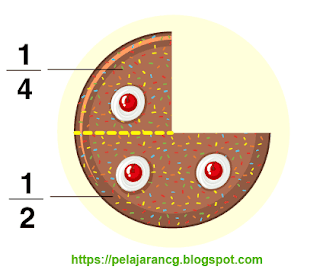
Pecahan adalah istilah yang dipakai untuk memilih bagian-bagian dari suatu benda secara keseluruhan. Contohnya, pizza dibagi menjadi empat bagian, sehingga setiap bagian direpresentasikan sebagai 1/4 bab dari pizza. Di sini 1 yakni pembilang dan 4 adalah penyebut.

Berdasarkan pembilang dan penyebutnya, selain ketiga jenis utama cuilan tersebut, ada tiga jenis potongan lagi ialah penggalan sejenis & tidak sejenis dan pecahan senilai. Oleh karena itu, ada total enam jenis bilangan bagian seperti yang hendak dijelaskan kurikulum pelajarancg.blogspot.com:

1. potongan murni,
2. bagian tak murni,
3. penggalan adonan,
4. kepingan sejenis,
5. penggalan tidak sejenis, dan
6. potongan senilai,

Catatan Pelajarancg: Tiga bilangan bagian pertama didefinisikan untuk belahan tunggal namun tiga cuilan lainnya, pastikan mempelajari perbandingan antara dua kepingan atau lebih.

Dalam skenario kehidupan sehari-hari, semua besaran yang diukur tidak dapat menjadi bilangan bundar mutlak, kita mungkin mesti bermasalah dengan bagian dan bilangan dari benda utuh, dan di sinilah rancangan cuilan timbul.

BERAGAM JENIS-JENIS BILANGAN PECAHAN

Bilangan Pecahan dianggap sebagai perbandingan dua bilangan. Angka atas disebut Pembilang, dan bab bawah disebut Penyebut. Ketika suatu keseluruhan dari sesuatu dibagi menjadi beberapa bagian, maka setiap bab disebut selaku potongan. Contoh tipikal bagaimana konsep cuilan melakukan pekerjaan diilustrasikan pada gambar di bawah ini kurikulum pelajarancg.blogspot.com:

Perhatikan teladan lain kurikulum pelajarancg, seluruh pizza dibagi menjadi delapan bab yang membentuk pecahan, di mana satu bab dari seluruh pizza direpresentasikan selaku 1/8, di mana 1 ialah pembilang dan 8 ialah penyebut.

bagian murni

Pecahan yang pembilangnya lebih kecil dari penyebutnya, maka disebut potongan murni biasa. adalah, Pembilang < Penyebut
Sebagai acuan,

Catatan Pelajarancg: Nilai penggalan biasa sehabis penyederhanaan lebih lanjut senantiasa kurang dari 1.

Pecahan tak murni

Pecahan yang pembilangnya lebih besar dari penyebutnya, maka disebut pecahan tak murni. yaitu, Pembilang > Penyebut

Sebagai teladan,

Catatan Pelajarancg:

• Semua bilangan asli atau murni dapat dinyatakan dalam bentuk cuilan, di mana penyebutnya selalu sama dengan 1.
• Penyederhanaan bagian biasa menciptakan nilai yang serupa atau lebih besar dari 1, tetapi tidak kurang dari 1.

Pecahan campuran

Pecahan campuran adalah kombinasi dari bilangan asli dan pecahan. Ini pada dasarnya adalah pecahan tak murni biasa. yaitu, Pembilang > Penyebut

Sebagai pola,

Catatan Pelajarancg:

• Bilangan Pecahan campuran selalu mampu diubah menjadi cuilan.
• Pecahan biasa dapat diubah menjadi Bilangan belahan adonan.
• Pecahan gabungan senantiasa lebih besar dari 1.

Pecahan sejenis

Bilangan pecahan yang penyebutnya sama disebut bagian sejenis. Contohnya 1/2, 3/2, 5/2, 7/2 mirip belahan.

Penyederhanaan cuilan tersebut mudah, alasannya adalah semua penyebut di sini ialah sama atau sejenis. Contoh kita perlu menjumlahkan semua penggalan sejenis di atas, maka;

1/2 + 3/2 + 5/2 + 7/2 = (1+3+5+7)/2 = 16/2 = 8

Pecahan tidak sejenis

Pecahan yang penyebutnya tidak sejenis atau penyebutnya berbeda disebut kepingan tak sama.

Contohnya 1/2, 1/3, 1/4, 1/5, tidak mirip potongan sejenis.

Penyederhanaan untuk bagian semacam itu adalah metode yang sedikit panjang karena kita perlu memfaktorkan penyebutnya terlebih dulu dan lalu menyederhanakannya (dalam hal penambahan dan pengurangan).

1. Contoh, kita harus menambahkan 1/2 dan 1/3. Maka pertama-tama kita akan mencari KPK dari 2 dan 3 yang sejenis atau sama dengan 6.
2. Sekarang kita perlu mengalikan 1/2 dengan 3 dan 1/3 dengan 2, baik pembilang maupun penyebutnya.
3. Pecahan menjadi 3/6 dan 2/6.
4. Sekarang kalau kita menyertakan 3/6 dan 2/6, kita mendapatkan;
5. 3/6+2/6 = 5/6

Pecahan senilai

Jika dua atau lebih serpihan mempunyai hasil yang serupa setelah disederhanakan dan mewakili bab yang serupa dari keseluruhan, maka penggalan tersebut sama satu sama lain dan disebut bagian senilai.

Contohnya, 1/2 dan 2/4 setara dan sejenis.

1/3 dan 3/9 adalah sejenis.

Contoh

Mari kita lihat beberapa teladan di sini berdasarkan jenis bagian pada bilangan.

• Contoh Pecahan murni: 2/3, 2/4, 2/5, 1/2. 4/7, 7/9, dst. (Pembilang < Penyebut)
• Contoh Pecahan tak murni: 3/2, 4/2, 5/2, 7/4, 9/7, 8/5, dst. (Pembilang > Penyebut)
• Contoh Pecahan Campuran: 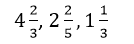dll. (Kombinasi bilangan lingkaran, Pecahan murni dan tak murni)

Untuk pengertian rancangan yang lebih baik, silakan pelajari dengan terus mengunjung blog kurikulum pelajarancg.blogspot.com