Integral Tertentu – Media Masyarakat

Daftar Isi

Definisi integral tertentu atau tentu

Integral tertentuadalah nilai dari jumlah luas dibawah suatu kurva tertentu dalam interval a ≤ x ≤ b, a disebut batas bawah dan b disebut batas atas integral tertentu. Sebelum pembahasan lebih jauh saya yakin anda sudah menguasai materi integral tak tentu, tapi kalau lupa silahkan direview lagi halaman lain blog ini, klik tulisan berwarna.

Integral tertentudituliskan dalam notasi $\int_{a}^ {b}f(x) \, dx$ disebut integral tertentu karena hasilnya berupa nilai tertentu dan tidak lagi mengandung konstanta.

Rumus dan Bentuk umum integral tertentu

http://soulmath4u.blogspot.com/2014/02/integral-tertentu.html

Soal-soal dan Pembahasan integral tertentu matematika kelas 12

Untuk memahami bagaimana cara menghitung integral tertentu, simak soal-soal dibawah ini!

Hitunglah nilai setiap integral tertentu dibawah ini!

(1). $\int_{1}^ {3}(4x^3+3x^2)\, dx$

[Penyelesaian]
$\\=\int_ {1}^{3}(4x^3+3x^2)\, dx\\\\=\left [ x^4+x^3 \right ]_{1}^ {3}\\\\=(3^4+3^3)-(1^4+1)=106$

(2). $\int_{1}^{4}(6x^2-\frac{2}{x^2})\, dx$

[Penyelesaian]

Ubah dahulu integran nya kedalam bentuk pangkat positif,
$\\=\int_{1}^{4}(6x^2-\frac{2}{x^2})\, dx=\int_{1}^{4}(6x^2-2x^{-2}) \\\\=\left [ 2x^3+\frac{2}{x} \right ]_{1}^{4} \\\\=(2.4^3+\frac{2}{4})-(2.1^3+2)=123,5$

(3). $\int_{1}^{4}\left ( x\sqrt{x} +\frac{1}{x\sqrt{x}}\right )^2\, dx$

[Penyelesaian]

Jabarkan terlebih dahulu integran nya dengan rumus kuadrat suku dua,

Untuk soal No 4 dan 5, tentukan nilai a jika diketahui:
$\\=\int_{1}^{4}\left ( x\sqrt{x} +\frac{1}{x\sqrt{x}}\right )^2\, dx \\\\=\int_{1}^{4}\left ( x^3+2+\frac{1}{x^3} \right )\, dx \\\\=\left [ \frac{1}{4}x^4+2x-\frac{1}{2x^2} \right ]_{1}^{4}$
$\\=\left [ \frac{1}{4}.4^4+2.4-\frac{1}{2.4^2} \right ]-\left [ \frac{1}{4}.1^4+2.1-\frac{1}{2.1^2} \right ]=70\frac{7}{32}$

(4). $\int _{0}^{a}\sqrt{x}\, \, dx=18$

[Penyelesaian]

Soal seperti ini merupakan variasi soal dari integral tertentu,
$\\\int _{0}^{a}\sqrt{x}\, \, dx=18 \\\\\int _{0}^{a}x^{\frac{1}{2}}\, dx=18 \\\\\frac{2}{3}\left [ x^{\frac{3}{2}} \right ]_{0}^{a}=18$
$\\\left [ x^{\frac{3}{2}} \right ]_{0}^{a}=27 \\\\a^{\frac{3}{2}}=27\\\\\therefore a=9$

(5). $\\\int_{-1}^{2a}\,\left (\frac{dx}{x^2} \right )=\frac{1}{2}$

[Penyelesaian]
$\\\int_{-1}^{2a}\,\left (\frac{dx}{x^2} \right )=\frac{1}{2} \\\\\int_{-1}^{2a}\, x^{-2}\, dx=\frac{1}{2} \\\\-\left [ \frac{1}{x} \right ]_{-1}^{2a}=\frac{1}{2}$

integral tertentu untuk menghitung luas Daerah Antara dua Kurva

Salah satu kegunaan integral tertentu adalah untuk menghitung luas antara dua buah kurva, yang tentu saja berbeda dengan menghitung luas bangun datar yang sudah jelas bentuk dan ukurannya.

http://soulmath4u.blogspot.com/2014/02/integral-tak-tentu.html

Misalkan fungsi f dan g adalah fungsi yang kontinu dalam interval [a,b] dan f(x) ≥ g(x), maka luas daerah antara kurva f(x) dan g(x) dapat dihitung dengan rumus:

Soal-soal dan Pembahasan integral tertentu Luas antara dua Kurva

Hitunglah luas daerah yang dibatasi oleh kurva dibawah ini!

(1). $y=x^2+3x\, \, dan\, \, y=2x+2$

[Penyelesaian]

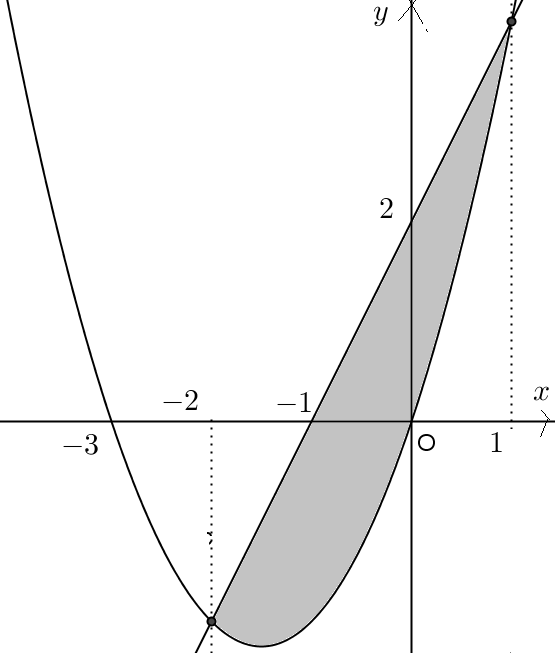
Tentukan terlebih dahulu titik potong antara dua kurva, untuk menentukan batas atas dan batas bawahnya.

$\\x^2+3x=2x+2 \\x^2+x-2=0 \\(x-1)(x+2)=0 \\x=1\, atau\, x=-2$

Jadi batas-batasnya adalah x = – 2 dan x = 1, maka luasnya adalah:
$\\L=\int_{-2}^{1}(2x+2)-(x^2+3x)\, dx \\\\ =\int_{-2}^{1}(-x^2-x+2)\, dx \\\\=\left [ -\frac{1}{3}x^3-\frac{1}{2}x^2+2x \right ]_{-2}^{1}$
$\\=(-\frac{1}{3}-\frac{1}{2}+2) -(\frac{8}{3}-2-4)\\\\=\frac{9}{2}\, satuan\, luas$

Integral Tertentu luas daerah dibawah sumbu x

Jika L adalah luas daerah yang dibatasi grafik f(x) dan f(x) ≤ 0, dalam interval a≤ x≤ b maka rumus menghitung luasnya adalah:

Luas daerah yang diarsir adalah:

Contoh soal:

Tentukan luas daerah yang dibatasi oleh kurva berikut ini dan sumbu x!

(1). Daerah yang dibatasi $y=x^2+x-2$ , dan sumbu x

[Penyelesaian]

Tentukan terlebih dahulu titik potong kurva dengan sumbu x,

$\\x^2+x-2=0\\\\(x-1)(x+2)=0 \\\\x=1\, \, atau\, \, x=-2$

Kurva merupakan fungsi kuadrat, jika lupa cara menggambar grafik dan menentukan titik potongnya lihat dulu langkah-langkah menggambar grafik fungsi kuadrat. Gambar grafik nya adalah:

Maka luas daerah yang diarsir,
$\\L=-\int_{-2}^{1}(x^2+x-2)\, dx \\\\=-\left [ \frac{1}{3}x^3+\frac{1}{2}x^2-2x \right ]_{-2}^{1}$
$\\=\left ( \frac{1}{3}.1^3+\frac{1}{2}.1^2-2.1 \right )-\left ( \frac{1}{3}.(-2)^3+\frac{1}{2}.(-2)^2-2.(-2) \right ) \\\\=4\frac{1}{2}$

(2). Daerah yang diabatasi oleh $y=-x^3-x^2+2x$ dan sumbu x

[Penyelesaian]

Tentukan terlebih dahulu titik potong kurva dengan sumbu x,
$\\-x^3-x^2+2x=0\\-x(x^2+x-2)=0 \\-x(x-1)(x+2)=0 \\x=0\, \, atau\, \, x=1\, \, atau\, \, x=-2$

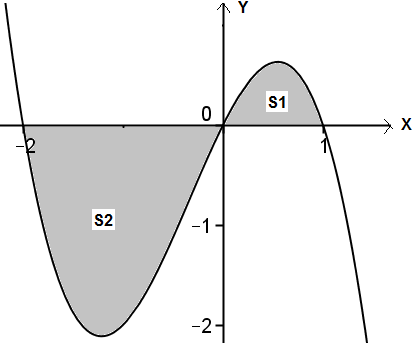
Grafik:

Dari grafik diatas terdapat dua daerah yang diarsir yaitu S1 dan S2 , dimana S2 berada dibawah sumbu x maka Luas daerah yang diarsir adalah:

$\\L=\int_{a}^{b}S_{1}\, dx-\int_{c}^{d}S_{2}\, dx \\\\L=\int_{0}^{1}(-x^3-x^2+2x)\, dx-\int_{-2}^{0}(-x^3-x^2+2x)\, dx \\\\L=\frac{37}{12}$

Semoga bermanfaat, mohon kritik dan saran dibagian komentar.Selamat belajar integral tertentu!

Materi Terkait :

□ Integral Tak Tentu

□ Integral parsial

□ Integral Kalkulus

□ Integral substitusi

□ Integral trigonometri