Ekstraksi Data Pada Halaman Web Menggunakan Partial Tree Alignment

Ekstraksi Data Pada Halaman Web Menggunakan Partial Tree Alignment

Web mining merupakan penggunaan teknik data mining untuk memperoleh dan mengekstrak berita dari dokumen dan layanan web . Tantangan dari web mining adalah jumlah isu yang banyak untuk mempermudah jalan masuk dengan pengembalian data baik online maupun offline dari source teks dari web . Penelitian web mining terintegrasi dengan berbagai macam penelitian disiplin ilmu pengetahuan yang lain seperti Database (DB),Datamining , Information Retrieval ,Machine Learning (ML),Natural Language Process (NLP). Web mining dapat dibagi menjadi tiga kategori utama yaitu : content mining , usage mining ,dan structure mining .

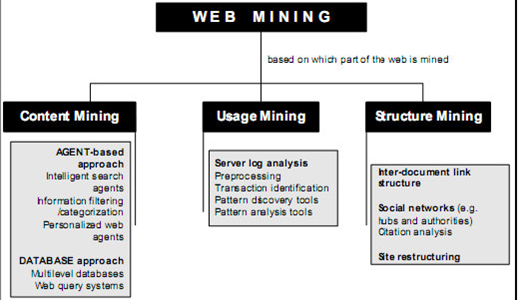
Gambar Taksonomi web mining

Pada peran akhir ini memfokuskan kepada web content mining. Web content mining yakni ,merupakan apliakasi untuk ,me-mining , mengekstrak dan memadukan data, gosip dan wawasan yang bermanfaat dari isi halaman web data web content tediri dari :

1. Unstructured data (teks bebas).

2. Semi structured data (dokumen HTML).

3. More structured data (data pada table, DB yang dihasilkan halaman HTML).

Pada intinya web content mining mendeskripsikan penemuan isu yang berkhasiat dari data, dokumen atau isi web pada halaman web. Ada dua cara pandang yang berlainan dalam melaksanakan observasi perihal web content mining, yaitu :

1. Cara pandang database: cara pandang ini mencoba untuk memodelkan data pada web dan mengintegrasikannya biar mampu dipakai sebaik-baiknya.

2. Cara pandang information retrieval: cara pandang ini membantu atau memperbaiki kualitas info yang didapatkan dalam web atau dengan kata lain menyaring isu didasarkan pada keinginan pemakai.

Gambar  Cara pandang web content mining 

Web content mining kadangkala disebut juga web text mining alasannya isi teks lebih sering dipakai sebagai observasi. Teknologi yang lazimnya digunakan web content mining adalah NLP dan IR [13] tetapi pada tugas selesai ini cuma memakai IR saja. Kegunaan web content mining pada World Wide Web antara lain mendapatkan info yang berhubungan dan menciptakan pengetahuan dari berita yang ada, sehingga gosip dalam jumlah yang banyak di situs web tetapi gampang untuk mengaksesnya. Informasi tersebut berupa semi-structured dengan aba-aba HTML, yang mana umumnya halaman web berisi adonan informasi seperti main content (isi utama), iklan, navigation panel, copyright notice, logo, dan lain-lain. Sedangkan pada tugas selesai ini akan memanfaatkan teks dalam hal ini cuma tag string pada HTML yang hendak di-mining. 

Konsep Mining Data Record

Ide pokok dari pemilihan algoritma MDR (Mining Data Records in web pages) pada tugas tamat ini alasannya adalah lebih efektif dan efisien daripada metode otomatis yang sudah ada yang lain, seperti OMINI dan IEPAD. Efektif sebab cuma melakukan dua observasi, ialah memperhatikan data record yang berada pada halaman web dan algoritma pencocokan string. Sedangkan efisien alasannya cuma melakukan pencocokan string pada node children yang satu parent saja, contohnya pada Gambar 5, tidak seperti data record mengawali dari TD* dan selsai di TD#. Berdasarkan observasi yang sudah ada dengan memakai algoritma MDR untuk me-mining data record pada halaman web mampu menghasilkan akurasi yang jauh lebih elok dibandingkan dengan OMINI dan IEPAD. 

Pada gambar 3 mampu dilihat pemahaman secara lazim sebuah data region dan sebuah data record. Sebuah data region adalah daerah yang sungguh berhubungan dari halaman web, mirip tempat pada situs web yang berisi sebuah daftar produk membentuk tempat data. Sebuah data record yakni sekumpulan data yang tolong-menolong merepresentasikan entitas mempunyai arti yang bangkit sendiri, seperti daftar produk dalam data region pada situs web. Algoritma MDR termasuk teknik unsupervised learning, ialah metode diberikan hanya satu halaman web dengan banyak data record, kemudian tata cara mengekstrak data secara otomatis.

Gambar  Halaman web yang menjelaskan data record dan data region

Menurut paper rujukan berasumsi bahwa data record pada halaman web biasanya terdapat pada tag HTML dalam bentuk yang berhubungan dengan tabel dan form, misalnya tag table, form, tr, td dan lain sebagainya. Pada tugas tamat ini, algoritma MDR didasarkan pada dua observasi, yakni:

Gambar  Halaman web dengan dua data record 

1. Data region (atau data record region) ialah sekumpulan data record berisi deskripsi dari golongan obyek serupa yang ditampilkan secara khusus pada halaman web dengan region berdekatan dan disusun menggunakan tag HTML yang sama. Seperti Gambar 4 diatas, dua notebook ditampilkan pada satu region yang berdekatan serta disusun menggunakan tag HTML. 

2. Struktur bersarang dari tag HTML pada halaman web lazimnya membentuk suatu tag tree dan sekumpulan data record serupa dibuat oleh beberapa node children dari sub-tree pada node parent yang sama. Contohnya pada Gambar 5, merupakan tag tree untuk halaman web pada gambar 4. Misalnya setiap notebook (atau sebuah data record) pada gambar 4 diekstrak ke dalam 5 node TR dengan bab tree di bawah node parent TBODY yang serupa pada Gambar 5, sehingga terdapat dua data record pada dua kotak garis putus-putus. 

Gambar  Contoh tag tree HTML dari halaman web pada Gambar 4 

Pada peran tamat ini, untuk melaksanakan teknik mining data record pada suatu halaman web terdapat tiga langkah, ialah:

1. Membangunan HTML tag tree.

2. Mining data region dalam halaman web dengan memakai tag tree dan perbandingan string. Mining data region dilakukan terlebih dulu, sebab sangat sukar dalam mining data record secara pribadi. Oleh alasannya adalah itu, mining data region dijalankan untuk menerima data record di dalam data region tersebut. Contohnya, pada Gambar 5, mendapatkan satu data region di bawah node TBODY.

3. Mengidentifikasi data record dari setiap data region. Contohnya, pada Gambar 5, langkah ini mendapatkan data record 1 dan data record 2 pada data region di bawah node TBODY.

Membangun HTML Tag Tree

Pada tugas simpulan ini, hanya memakai tag-tag dalam perbandingan string untuk menemukan data record. Kebanyakan tag-tag HTML bekerja dalam pasangan. Setiap pasang berisikan suatu tag pembuka (opening tag) dan sebuah tag epilog (closing tag), masing-masing diindentifikasi dengan “< >” dan “”. Dalam setiap pasangan tag mampu berafiliasi dengan pasangan tag lainnya, sehingga menimbulkan blok bersarang pada aba-aba HTML. Pembangunan sebuah tag tree dengan menggunakan instruksi HTML secara natural. Pada tag tree, setiap pasang dari tag diperhitungkan menjadi satu node.

Mining Data Region

Langkah ini yaitu me-mining setiap data region pada halaman web yang berisi data record serupa, tetapi tidak dapat me-mining data record secara pribadi, alasannya susah, pertama kali yang dilaksanakan ialah me-mining node generalized pada halaman web. Sekumpulan node generalized yang berdekatan membentuk sebuah data region. Dari setiap data region, akan mengidentifikasi data record yang sebetulnya.

Node generalized (atau sebuah node kombinasi) dengan panjang r dimana terdiri dari r (r > 1) node pada HTML tag tree dengan dua karakteristik sebagai berikut:

1. Semua node yang memiliki parent yang serupa.

2. Node-node yang berdekatan.

Node generalized menerangkan bahwa sebuah obyek (atau data record) mungkin terisi dalam node-node tag sibling yang jumlahnya lebih daripada satu. Node generalized berlawanan dengan node tag. Sedangkan node tag ialah setiap node tag pada tag tree pada Gambar-5.

Data region ialah kumpulan dari dua atau lebih node generalized dengan mempunyai beberapa karakteristik selaku berikut :

1. Semua node generalized mempunyai parent yang sama.

2. Semua node generalized memiliki panjang yang sama.

3. Semua node generalized yang berdekatan.

4. Normalisasi edit distance (perbandingan string) antara node generalized yang berdekatan lebih kecil daripada batas-batas yang sudah ditentukan.

Pada Gambar, memperlihatkan bahwa mampu membentuk dua node generalized. Pertama terdiri 5 node children dari TR permulaan untuk TBODY, dan kedua adalah 5 node children dari TR selanjutnya untuk TBODY. Meskipun node generalized pada data region mempunyai panjang yang serupa (mempunyai jumlah node children yang sama dari satu parent pada tag tree) namun node dengan level terbawahnya dapat sangat berlawanan.

Perbedaan antara node generalized dengan data region diterangkan pada Gambar-6 dengan memakai suatu tag tree produksi dan nomer ID yang menggambarkan node tag pada tag tree. Daerah gelap ialah node generalized. Node 5 dan 6 yakni node generalized dengan panjang 1 dan mendefinisikan data region dengan label 1 kalau keadaan edit distance terpenuhi. Node 8, 9, dan 10 yaitu node generalized dengan panjang 1 dan mendefinisikan data region dengan label 2 kalau kondisi edit distance tercukupi. Pasangan dari node (14, 15), (16, 17) dan (18, 19) yakni node generalized dengan panjang 2 dan mendefinisikan data region dengan label 3 jikalau keadaan edit distance tercukupi.

Gambar  Ilustrasi dari node generalized dan data region 

Pada peran final ini, mengasumsikan bahwa node-node membentuk sebuah data region dari parent yang sama. Contohnya, tidak seperti data region dimulai dari node 7 dan akan selsai pada node 14. Sebuah node generalized mungkin bukan mempresentasikan suatu data record, namun itu digunakan untuk mendapatkan data record.

Mengidentifikasi Data records

Data yang sudah terbentuk dalam region-region (direpresentasikan dengan node generalized ) sungguh beragam kombinasinya ,berikut 2 kasus utama dalam mengidentifikasi data record

1. Non – Contiguous Data Records : Case 1

Dalam beberapa halaman web dalam mendeskripsikan sebuah data object (record) tidak dapat dianalisis kedekatannya berdasarkan HTML code-nya(contiguous segment) . Amati dalam gambar berikut

Multiple-record data region: masing-masing node terdiri lebih dari satu non-contiguous data record

Dalam kasus ini ,data regions berisikan dua generalized nodes, dimana masing-masing generalized nodes berisikan dua tag nodes (dua rows), yang mengindikasikan bahwa dua tag node (rows) tersebut diatas tidak ada kesamaan satu sama lain . Tetapi masing-masing tag node memiliki jumlah children node yang serupa dan children node ini memiliki kesamaan satu sama lain. 

Untuk masalah ini kita dapat menulisnya menjadi satu row lists untuk nama yang diambil dari dua object dalam dua cells dan row lists selanjutnya. Sehingga mampu ditulis name 1,name 2,description 1,description 2,name 3,name 4, description 3, description 4.

Non-Contiguous Data Records:Case 2

Bentuk adjecent data regions yang mempunyai lebih dari satu non-contiguous data records 

Kasus diatas berisikan dua atau lebih data regions dari multiple data records ,diamana dalam gambar diatas row 1 dan row 2 tidak mempunyai kesamaan satu sama lain, dimana bentuk row 1 dari sebuah data regions dan bentuk row 2 berasal dari data region yang berbeda. 

DATA EXTRACTION

Dalam data extraction ini kita akan menerapkan sebuah teknik yang dinamakan dengan partial tree alignment , yang kunci pokoknya yaitu bagaimana mencocokkan corresponding data item atau field dari data semua data records. Ada dua langkah penting dalam data extraction:

1. Membuat satu root tag tree untuk masing-masin data record :

Setelah semua data record telah teridentifikasi, sub-trees pada masing data records di susun ulang ke dalam single tree .Masing-masing data record ada kemungkinan mempunyai lebih dari satu sub-trees dari sebuah original tag tree pada suatu halaman , dan masing-masing data record mungkin tidak memiliki kesamaan (Case 1 dan Case 2 pada perkara Pengidentifikasian data record). Sub-step ini diharapkan untuk menyusun single tree untuk masing-masing data record(suatu root node buatan yang dapat di tambah setiap dikala). 

2. Partial tree aligment: tag trees dari semua data dalam masing-masing data region di aligned memakai tata cara partial alignment berdasarkan tree matching

Dalam data extraction akan melalui banyak sekali tahapan yakni selaku berikut:

Tree Edit Distance

Tahap tree edit distance adalah mengukur kesamaan antara dua trees A dan B(root trees yan telah terlabel terurut ) berdasarkan cost dalam sebuah minimum set dari operasi yang diperlukan untuk mentransform A kedalam B. Menurut formula klasik,kumpulan dari operasi yang dipakai untuk memilih tree edit distance budpekerti tiga tahap: node removal,node insertion ,node replacement. Sebuah cost umumnya di assign terlebih dahulu pada masing-masing operasi. 

Masalah tree edit distance adalah inovasi minimum-cost mapping antara dua tree ,berikut yaitu salah satu contoh konsep mapping tersebut diatas:

Misalkan X yakni tree dan misalkan X[i] adalah node ke-i dari tree X dalam tahapan preorder . Mapping M antara tree A yang berukuran n1 dan tree B yang berskala n2 yakni kumpulan dari pairs(i,j) yang telah terurut dari setiap tree ,berikut yaitu algoritma untuk keadaan (i1,j1)(i2,j2) ε M :

(1) i1 = i2 iff j1 = j2;

(2) A[i1] is on the left of A[i2] iff B[j1] is on the left B[j2];

(3) A[i1] is an ancestor of A[i2] iff B[j1] is an ancestor of B[j2].

Masing-masin node dihilangkan satu kali saat melaksanakan mapping dan diurutkan antara sibling node dan hierarichal relation antara kedua node yang sudah ada. Berikut yaitu gambar yang membuktikan mapping .

Berikut beberapa algoritma yang telah dilakukan untuk mencari minimum set dari operasi untuk men-transform satu tree ke dalam lainnya,dimana dalam setiap formula mempunyai kompleksitas kuadratik(O(n1n2h1h2)), dimana n1 dan n2 ukuran sebuah tree dan h1 dan h2 yakni kedalaman suatu tree hal ini juga ditunjukan pada masalah tree yang tidak terurut. 

Simple Tree matching 

Pada umumnya mapping mampu dilaksanakan antara node a di tree A dan node b di tree B secara silang ,disini juga terdapat replacement node b di dalam A node h di dalam B. Dalam masalah ini kita memakai restricted matching algorithm ,yang pertama di ajukan untuk membandingkan dua acara computer dalam software engineering.Algoritma ini disebut dengan simple tree matching (STM). STM ini mengevaluasi similarity dari dua trees yang menghasilkan maximum matching dalam suatu dynamic programming dengan complexity O(n1.n2),dimana n1 dan n2 ukuran dari trees A dan B (tidak memakai replacement dan no level crossing masih diijinkan). 

Missal A dan B dua buah tree dan i ε A,j ε B adalah node di A dan B .A matching antara dua trees ditujukan untuk mapping M dimana setiap pasangan (i,j) ε M dan i dan j yakni non-root nodes , (parents(i),parent(j)) ε M . A maximum matching yaitu matching dengan jumlah pairs maximum.

Misal A = dan B =< RB,B1,B2,…Bm > dua trees ,dimana RA dan RB adalah root dari A dan B dan Ai,Aj ialah level pertama sub trees ke i dan j dari A dan B . ketika RA dan RB terdiri dari identical symbol , maximum matching antara A dan B yakni MA,B+1 ,dimana MA,B yaitu maximum matching antara < A1,A2,…Am> dan . MA,B mampu diperoleh dari dynamic programming scheme:

1. Jika maximum matching antara Am dan Bm lebih besar dari pada maximum matching antara Am dan Bi(1≤iMA,B yakni maximum matching antara < A1,A2,…Am-1> dan ditambah maximum matching antara Am dan Bm.

2. Terkadang , MA,B adalah maximum matching antara < A1,A2,…Am> dan atau antara < A1,A2,…Am-1> dan

Dalam algoritma Simple tree matching , root dari A dan B dibandingkan pertama kali (line 1). Jika root terdiri dari distinct symbol maka dua tree tersebut tidak mempunyai kesamaan sama sekali. Jika root berisikan identical symbol maka algoritma STM secara recursive memperoleh maximum matching antara first-level sub-trees dari A dan B dan menyimpan kesudahannya dalam matriks W (line 8). Berdasarkan pada matriks W , dynamic programming maximum matching antara dua tree A dan B.

1. Algorithm: Simple_Tree_Matching(A, B)

2. if the roots of the two trees A and B contain distinct symbols

3. then return (0);

4. else m:= the number of first-level sub-trees of A;

5. n:= the number of first-level sub-trees of B;

6. Initialization: M[i, 0]:= 0 for i = 0, …, m;

7. M[0, j] := 0 for j = 0, …, n;

8. for i = 1 to m do

9. for j = 1 to n do

10. M[i,j]:=max(M[i,j-1], M[i-1, j], M[i-1, j-1]+W[i, j]);

11. where W[i,j] = Simple_Tree_Matching(Ai, Bj)

12. endfor;

13. endfor;

14. return (M[m, n]+1)

15. endif

(A) Tree A; (B) Tree B; (C) M matrix for the first level sub-trees of N1 and N15; (D) W matrix for the first level sub-trees of N1 and N15; (E)-(H) M matrixes and W matrixes for the lower level sub-trees.

Untuk mendapatkan maximum matching antara tree A dan B ,dimana rootnya ,N1 dan N15 sudah dulu dibandingkan (compared first). Seteleh N1 dan N15 sudah masuk kedalam identical symbol , nilai M1-15[4,2]+1 dikembalikan selaku nilai maximum matching antara tree A dan B (line 11) . M1-15 di hitung menurut pada matriks W1-15 dan masing-masing nilai masukan dalam W1-15 ,lalu dikatakan bahwa W1-15 [i,j] ialah maximum matching antara first-level sub-trees ke i dan ke j pada A dan B ,dimana secara recursive dihitung berdasarkan matriks M . Contoh W1-15 [4,2] dihitung secara recursive dengan membangun matriks (E)-(H) ,semua cell yang relevant akan dikumpulkan .Matriks M akan di inisialisasi dengan mengisi nilai nol pada column dan row nya.(Note : untuk matriks M dan W yang sedang dalam penghitungan diberi garis bawah ).

Selama proses matching (atau sehabis proses matching) ,kita dapat men-trace back matriks M untuk mendapatkan node yang sesuai atau memiliki kesamaan(matched /aligned) dari dua tree,dikala mendapatkan lebih dari satu yang sesuai untuk node yang menunjukkan nilai maximum. Kemudian kita pilih satu yang terendah kedalamannya dalam tree. Contoh ,node c dalam tree A mampu dilakukan pencocokan pada waktu pertama atau selesai node c pada tree B, sesudah itu pilih node c yang pertama dalam B . heuristic ini dipakai untuk visual effectiveness dalam halaman web. Jika sebuah node yang paling akrab yaitu node x dalam tree A cocok maka lanjutkan pada node y pada tree B ,umumnya akan terdapat beberapa tag sebelum x. Heuristic ini sejauh ini telah efektif dalam beberapa experiment.

Two trees with more than one possible match

Multiple Alignment

Setiap data region yang mempunyai multiple data record pada sebuah halaman selain akan dilaksanakan proses align memakai multiple tag trees , juga akan dimasukan ke dalam suatu single table dalam database yang berkorespondensi satu sama lain dengan data items/field dalam kolom yang sama dalam table.Dimana data table ini masing-masing rownya merepresentasikan dalam sebuuh tree(data record),dan masing-masing kolomnya merepresnetasikan data field di masing-masing data record. 

Berikut ini yaitu salah satu algoritma yang ada untuk menanggulangi multiple sequences / trees yakni Multiple alignment method , Multiple alignment method yaitu sebuah metode yang memakai multidimensional dynamic programming ,tata cara ini sudah maksimal tetapi memerlukan kompleksitas waktu yang besar (exponential) dan tidak simpel,dan banyak juga tata cara heuristic untuk mengatasi persoalan ini salah satunya adalah Center string method yang hendak digunakan dalam multiple sequence alignment untuk mengatasi problem particular heuristic method .

Dalam Center string method ,sequence adalah xc dimana minimasinya adalah (D(xi,xc) yaitu jarak antara dua String) ∑ D(xi,xc) ,kemudian pair-wise alignment ditunjukan dalam (xi,xc) dimana i≠c . Asumsi ada k sequences dan semua sequences mempunyai panjang n ,waktu untuk memperoleh center O(k2n2) dan waktu masing-masing langkah iterative pada pair-wise alignment adalah O(n2) . Dapat dibilang untuk time costnya yakni O(k2n2).

Dalam mengukur similarity, kita tentukan center tree Tc dan meng-align tree yang lain dengan Tc ,ada dua cara untuk mengimplementasikan teknik ini 

Pertama ,walaupun pada setiap algoritma memiliki waktu kompleksitas polynomial , tetapi berlangsung dengan lambat untuk halaman yang terdiri pada banyak data record atau data record yang mempunyai banyak atribut. 

Yang kedua ,jikalau center tree tidak memiliki bagian data item ,data record lainnya yang berisikan data yang serupa pada center tree tidak butuhmengalami proses alignment . 

Partial Tree Alignment

Partial Alignment of two trees

Missal dua buah tree Ts dan Ti telah melaksanakan proses matching ,beberapa node Ti dilakukan proses align dengan menghubungkan node dalam Ts (saling sama satu sama lain).untuk setiap node Ti yang tidak cocok akan dimasukan ke dalam Ts . Ada dua kemungkinan saat memasukan node ni dari Ti ke dalam seed tree Ts tergantung apakah lokasi dalam Ts sungguh-sungguh unik untuk dimasukan node ni .Faktanya disini bukan hanya membandingkan dalam single node ni , hal ini di kerjakan untuk menangani kalau ada node yang unmatched masuk kedalam parent dari Ti (ni .. nj).

Assumsi bahwa parent node (ni .. nj) mempunyai kecocokan dalam Ts dan kita ingin memasukan (ni .. nj) kedalam Ts dibawah node parentnya. Kita cuma dapat memasukan (ni .. nj) kedalam Ts kalau posisi untuk memasukan (ni .. nj) adalah bersifat unik dalam Ts . Sebaliknya kita tidak akan mampu memasukan kedalam Ts dan unalignment kiri yang bersifat partial.

Untuk menentukan lokasi unik agar kita mampu memasukan node (ni .. nj) 

1. Jika (ni .. nj) mempunyai dua tetangga sibling dalam Ti ,satu di segi kanan dan satu di segi kiri yang tepat dengan consecutive sibling pada Ts . gambar dibawah ini akan menunjukan kondisi ini, yang memperlihatkan satu bab pada Ts dan satu bab dalam Ti . Kita mampu menyaksikan node c dan node d (consecutive sibling) dalam Ti dan dimasukan kedalam Ts antara node b dan e (matched ) .

2. Jika (ni .. nj) mempunyai satu tetangga kiri x dalam Ti dan x cocok dengan node kanan x dalam Ts ,kemudian (ni .. nj) dimasukan setelah node x dalam Ts.

3. Jika (ni .. nj) memiliki satu tetangga kanan x dalam Ti dan x cocok dengan node kiri x dalam Ts ,lalu (ni .. nj) dimasukan sebelum node x dalam Ts.

Terkadang kita tidak mampu memiliki lokasi node yang tidak unik untuk proses pencocokan node antara Ti dan Ts

Figure 1 Expanding the seed tree: (A) and (B) Unique expansion; (C) Insertion ambiguity.

Full Algorithm

Algorithm PartialTreeAlignment(S)

1. Sort trees in S in descending order according to the number of data items that are not aligned;

2. Ts = the first tree (which is the largest) and delete it from S;

3. flag = false; R = ∅; I = false;

4. while (S ≠ ∅)

5. Ti = select and delete next tree from S;

6. Simple_Tree_Matching(Ts, Ti);

7. L = alignTrees(Ts, Ti); // based on the result from line 6

8. if Ti is not completely aligned with Ts then

9. I = InsertIntoSeed(Ts, Ti);

10. if not all unaligned items in Ti are inserted into Ts then

11. Insert Ti into R;

12. endif;

13. endif;

14. if (L has new alignment) or (I is true) then

15. flag = true

16. endif;

17. if S = ∅ and flag = true then

18. S = R; R = ∅;

19. flag = false; I = false

20. endif;

21. endwhile;

22. Output data fields from each Ti to the data table based on the alignment results.

Ilustrasi