Bangkit Datar: Pengertian, Macam, Sifat, Rumus, Soal

Artikel kali ini akan membicarakan mengenai berdiri datar.

Salah satu materi yang terdapat dalam matematika yaitu geometri. Bangun datar merupakan salah satu topik yang ada dalam geometri.

Dengan mempelajari bangkit datar, kalian dapat menerapkannya untuk menyelesaikan persoalan dalam kehidupan sehari-hari.

Lalu, apa itu bangun datar?

Simak penjelasan tentang pengertian bangkit datar berikut.

Pengertian Bangun Datar

Bangun datar merupakan salah satu topik yang mempelajari objek atau bentuk berupa dua dimensi.

Bangun dua dimensi merupakan bangun yang memiliki keliling dan luas, namun tidak memiliki isi (volume). Bangun datar banyak diterapkan dalam kehidupan sehari-hari.

Simak klarifikasi di bawah ini.

Bangun Datar dalam Kehidupan Sehari-Hari

Bangun datar sudah banyak dipraktekkan dalam kehidupan sehari-hari. Beberapa contoh penerapannya yakni bentuk ubin yang menyerupai bangun persegi dan sisi meja mirip bentuk persegi panjang.

Selain itu, dikala kalian bermain layang-layang, objek layang-layang menyerupai bangun layang-layang, dan masih banyak penerapan bangkit datar yang yang lain.

Konsep terkait keliling dan luas berdiri datar juga banyak dipraktekkan untuk menyelesaikan problem sehari-hari.

Berikutnya akan dijelaskan mnegenai macam-macam bangkit datar.

Macam-Macam Bangun Datar

Perhatikan gambar berikut.

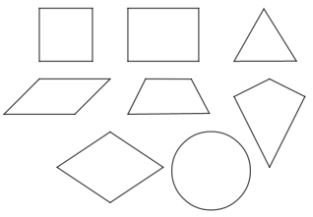
Pada gambar di atas terdapat macam-macam berdiri datar seperti berdiri persegi, persegi panjang, segitiga, jajar genjang, trapesium, belah ketupat, layang-layang, dan lingkaran.

Pembahasan berikutnya yaitu terkait sifat-sifat berdiri datar.

Sifat-Sifat Bangun Datar

Berikut merupakan sifat-sifat bangun datar.

1. Persegi

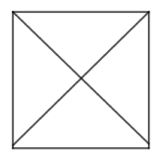
Sifat-sifat persegi adalah sebagai berikut.

• Memiliki empat segi yang sama panjang (dua pasang sisi yang sejajar).
• Mempunyai empat sudut siku-siku.
• Memiliki dua diagonal yang saling berpotongan tegak lurus.

Baca Selengkapnya di Persegi

2. Persegi Panjang

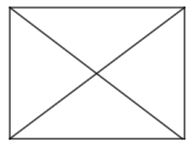
Sifat-sifat persegi panjang ialah selaku berikut.

• Memiliki dua pasang segi yang sejajar dan sama panjang.
• Keempat sudutnya siku-siku.
• Memiliki dua diagonal yang sama panjang.

Baca Selengkapnya di Persegi Panjang

3. Segitiga

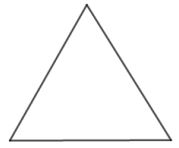
Berdasarkan panjang sisinya, bangun datar segitiga dibedakan menjadi tiga, yaitu segitiga sama segi, segitiga sama kaki, dan segitiga sembarang.

a. Segitiga Sama Sisi

Sifat-sifat segitiga sama sisi yaitu sebagai berikut.

• Ketiga sisinya sama panjang.
• Ketiga sudutnya sama besar (60°).

b. Segitiga Sama Kaki

Sifat-sifat segitiga sama kaki yaitu sebagai berikut.

• Dua dari tiga sisinya sama panjang.
• Memiliki sepasang sudut yang serupa besar.

c. Segitiga Sembarang

Sifat-sifat segitiga sembarang adalah sebagai berikut.

• Ketiga sisinya tidak sama panjang
• Ketiga sudutnya tidak sama besar

Berdasarkan besar sudutnya, bangkit datar segitiga dibedakan menjadi tiga, yaitu segitiga sama siku-siku, segitiga lancip, dan segitiga tumpul.

a. Segitiga Siku-Siku

Sifat-sifat segitiga siku-siku ialah sebagai berikut.

• Memiliki sudut terbesarnya yakni sudut siku-siku (90 derajat).

b. Segitiga Lancip

Sifat-sifat segitiga lancip ialah sebagai berikut.

• Ketiga sudutnya merupakan sudut lancip.

c. Segitiga Tumpul

Sifat-sifat segitiga tumpul adalah sebagai berikut.

• Salah satu sudutnya ialah sudut tumpul.

Baca Selengkapnya di Segitiga

4. Jajar Genjang

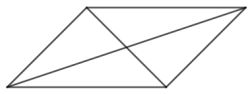
Sifat-sifat jajar genjang ialah selaku berikut.

• Memiliki dua pasang segi yang sejajar dan berhadapan sama panjang.
• Memiliki dua pasang sudut yang berhadapan sama besar.
• Memiliki dua diagonal yang membagi jajar genjang menjad dua sama besar.

Baca Selengkapnya di Jajar Genjang

5. Trapesium

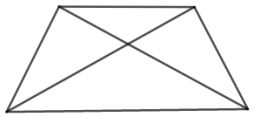
Sifat-sifat trapesium yaitu selaku berikut.

• Memiliki sepasang segi sejajar
• Memiliki dua pasang sudut sama besar (trapesium sama kaki) atau  memiliki dua sudut siku-siku (trapesium siku-siku).
• Jumlah besar sudut yang berdekatan di antara dua garis sejajar yaitu 180 derajat.

Baca Selengkapnya di Trapesium

6. Layang-Layang

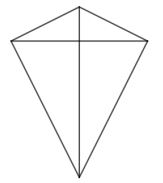
Sifat-sifat layang-layang adalah selaku berikut.

• Memiliki sepasang sudut yang serupa besar.
• Memiliki dua pasang sisi yang sama panjang.

Baca Selengkapnya di Layang-layang

7. Belah Ketupat

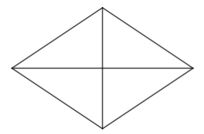
Sifat-sifat belah ketupat ialah selaku berikut.

• Memiliki empat sisi yang serupa panjang.
• Memiliki dua pasang sudut yang berhadapan sama besar.
• Diagonalnya saling berpotongan tegak lurus.

Baca Selengkapnya di Belah Ketupat

8. Lingkaran

• Memiliki satu titik pusat.
• Jarak sembarang titik pada bulat kepada pusat yakni sama.

Baca Selengkapnya di Lingkaran

Selanjutnya akan dibahas perihal banyaknya simetri putar pada bangkit datar.

Simetri Putar Bangun Datar

Simetri putar mampu diartikan selaku banyaknya posisi yang ibarat bentuk awal kalau diputar dalam satu putaran penuh. Berikut merupakan banyaknya simetri putar pada bangkit datar.

Bangun Datar	Banyak Simetri Putar
Persegi	4
Persegi panjang	2
Segitiga: Segitiga sama segi Segitiga sama kaki Segitiga sembarang	311
Jajar genjang	2
Trapesium: Trapesium sama kaki Trapesium siku-siku Trapesium sembarang	111
Layang-layang	1
Belah Ketupat	2
Lingkaran	tak terhingga

Selanjutnya akan dibahas tentang rumus bangkit datar.

Rumus Luas Bangun Datar

Pada pembahasan bagian ini akan dibahas rumus luas bangun datar. Berikut penjelasannya.

Luas bangkit datar ialah area/kawasan yang dibatasi oleh garis atau sisi-segi berdiri datar. Berikut ialah rumus luas bangkit datar.

L = ½ x a x t

Keterangan
a  : ukuran bantalan segitiga
t  : ukuran tinggi segitiga

Bangun Datar	Rumus Luas
Persegi	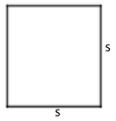L = s x s Keterangan s : ukuran segi persegi
Persegi panjang	L = p x l Keterangan p : ukuran panjang persegi panjang l  : ukuran lebar persegi panjang
Segitiga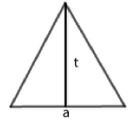
Jajar genjang	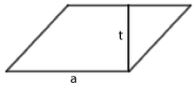L = a x t Keterangan a  : ukuran ganjal jajar genjang t  : ukuran tinggi jajar genjang
Trapesium	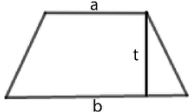L = ½ x (a + b) x t Keterangan a, b : ukuran sisi-segi sejajar trapezium t   : tinggi trapesium
Layang-layang	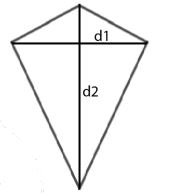L = ½ x d1 x d2 Keterangan d1, d2 : ukuran diagonal layang-layang
Belah Ketupat	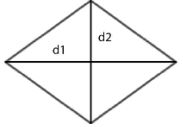L = ½ x d1 x d2 Keterangan d1, d2 : ukuran diagonal belah ketupat
Lingkaran	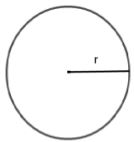L = π x r x r Keterangan r  : ukuran jari-jari bulat π  : konstanta (22/7 atau 3,14)

Coba lakukan soal berikut untuk meningkatkan pemahaman kalian tentang bangun datar.

Contoh Soal Bangun Datar

1. Tentukan luas bangkit datar berikut.

• Persegi dengan ukuran segi 8 cm.
• Persegi panjang dengan ukuran panjang 12 cm dan lebar 4 cm.
• Segitiga dengan ukuran ganjal 7 cm dan tinggi 6 cm.
• Jajar genjang dengan ukuran ganjal 5 cm dan tinggi 8 cm.
• Trapesium dengan ukuran sisi sejajar 12 cm dan 6 cm, serta tinggi trapesium 5 cm.
• Belah ketupat dengan ukuran diagonalnya 12 cm dan 9 cm.
• Layang-layang dengan ukuran diagonalnya 6 cm dan 14 cm.
• Lingkaran dengan jari-jari 14 cm.

2. Perhatikan gambar berikut.

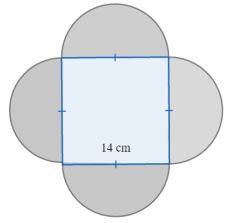
Tentukan luas bangkit campuran di atas.

Mari kita simpulkan  materi bangkit datar.

Kesimpulan

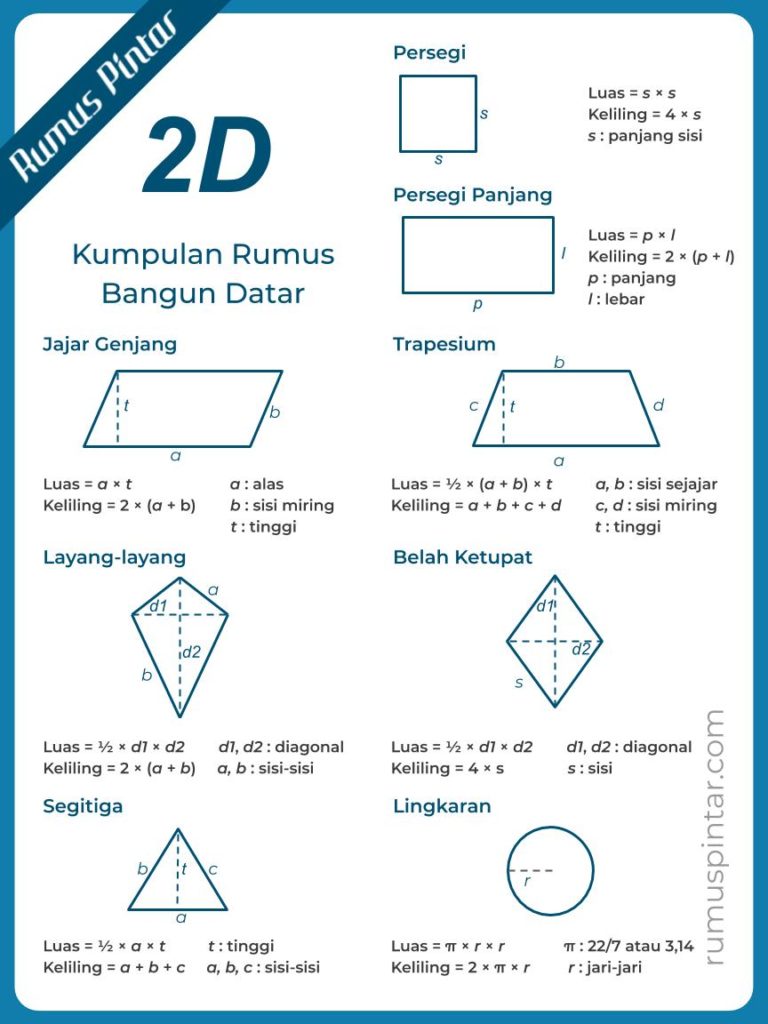
Bangun datar ialah bangun objek atau bentuk berbentuk dua dimensi. Bangun dua dimensi merupakan bangun yang mempunyai keliling dan luas, tetapi tidak mempunyai isi (volume).

Beberapa bangun datar ialah persegi, persegi panjang, segitiga, jajar genjang, trapesium, belah ketupat, laying-layang, d
an lingkaran.

Simetri putar dapat diartikan selaku banyaknya posisi yang menyerupai bentuk permulaan bila diputar dalam satu putaran sarat .

Demikian pembahasan perihal bangun datar, biar berguna.