Halo sahabat Next Generation, di peluang kali ini kita akan membahas bahan perihal hukum Bernoulli.simak materinya yaa.
Daftar Isi
Pengertian Hukum Bernoulli
Ketika kita mencar ilmu perihal fluida dinamik, pastinya kita akan mempelajari tentang hukum bernoulli.
Dimana ketika terdapat pipa horizontal dengan luas penanmpang yang berlainan dan pada setiap luas penampang yang berlawanan tersebut terdapat pipa penyangga vertical yang saling berhubungan dan berisi zat cair (air).
Maka, tinggi permukaan air yang ada di dalam pipa vertical tidak akan sama. Hal ini disebabkan karena ketinggian zat cair pada pipa vertical dipengaruhi oleh luas penampang pipa horizontal.
Luas penampang pipa horizontal yang lebih besar akan menciptakan tekanan yang besar pula, sehingga mengakibatkan tinggi air pada pipa vertikal lebih rendah daripada tinggi air pada pipa vertical dengan pipa horizontal yang luas penampangnya kecil.
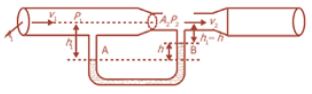
Sesuai dengan asas kontinuitas yakni dikala air mengalir pada pipa yang luas penampangnya kecil, maka akan mempunyai kecepatan yang besar.
Kemudian Daniel Bernoulli menyimpulkan bahwa “pada fluida yang engalir dengan kecepatan lebih tinggi akan diperolah tekanan yang lebih kecil”.
Bila dilihat dikala fluida bergerak pada ketinggian dan juga luas penampang yang berbeda akan tampak mirip pada gambar berikut.
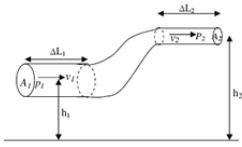
Bila ditinjau secara mekanika, pada ketinggian h2 energi potensial yang dimiliki fluida jauh lebih besar ketimbang energy berpotensi yang dimiliki fluida pada ketinggian h1.
Sehingga Bernoulli mengatakan bahwa tekanan pada fluida kian kecil bila terjadi penambahan ketinggian pada pipa.
Sehingga mampu disimpilkan tekanan fluida pada ketinggian h2 lebih rendah dengan tekanan fluida pada ketinggian h1.
Baik, sehabis pembahasan desain hukum Bernoulli kita akan membahas tentang persamaan aturan Bernoulli. Berikut pembahasannya.
Baca juga Induksi Elektromagnetik.
Persamaan Hukum Bernoulli
Dalam persamaan Hukum Bernoulli membahas kekerabatan antara tekanan fluida, kecepatan fluida, dan perbedaan ketinggian penampang yakni tetap. Perumusannya selaku berikut.
P + 1/2ρv2 + ρgh = tetap
Keterangan
- P = tekanan fluida
- v = kecepatan fluida mengalir
- h = selisih ketinggian penampang
karena dikatakan tetap, maka perumusan juga dapat ditulis mirip berikut
P1 + 1/2ρv 1 2 + ρgh1 = P2 + 1/2ρv 2 2 + ρgh2
setuju temen-temen, stelah kita mengetahui perumusan aturan Bernoulli kita akan lanjut ke pembahasan penerpan aturan Bernoulli dalam kehidupan sehari-hari.
Hukum Bernoulli Dalam Kehidupan Sehari-hari
Bila dalam kehidupan sehari-hari, penerpan hukum Bernoulli dapat dilihat pada
- Gaya angkat pada kedua sayap peswat melayang
- Tabung pitot
- Tabung venturi
- Alat karburasi sepeda motor
- Alat Penyemprot nyamuk
Nah temen-temen, selanjutnya akan dibahas contoh soal dari aturan Bernoulli. Simak dipoin berikut yaa.
Baca juga Rangkaian Listrik.
Contoh soal hukum bernoulli
1. Sebuah penampung air yang cukup besar memiliki ketinggian permukaan air 70 cm dari dasar penampung air. Ternyata penampung air tersebut mempunyai lubang pada dasarnya sebab telah termakan usia.
Berapa besar kecepatan fatwa air pada lubang tersebut?
Diketahui :
h1 = 70 cm = 0,7 m
P1 = P2 ; v1 = 0
ρair = 1000 Kg/m3
g = 10 m/s2
Ditanya: v2 = ?
Penyelesaian
P1 + 1/2ρv 1 2 + ρgh1 = P2 + 1/2ρv 2 2 + ρgh2
P1 + 0 + ρ.g(0.7m) = P2 + 1/2ρv 2 2 + 0
ρ.g(0.7m) = 1/2ρv 2 2
10.(0.7m) = 1/2v 2 2
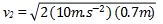
v2 = 3,74 m/s
2. Dua pipa yang terhubung memiliki luas penampang yang berbeda. Bila terdapat air yang melalui pipa tersebut maka kecepatan pada penampang 1 sebesar 3 m/s dengan P1 = 12300 Pa, sedangkan jikalau melewati penampang 2 kecepatan airnya sebesar 0.75 m/s. penampang 2 1,2 m lebih tinggi dibandingkan penampang 1.
Tentukan besar tekanan pada penampang 2!
Diketahui :
- v1 = 3 m/s
- P1 = 12300 Pa
- v2 = 0.75 m/s
- h2 = 1.2 m
- g = 9,8m/s2
Penyelesaian
P1 + 1/2ρv 1 2 + ρgh1 = P2 + 1/2ρv 2 2 + ρgh2
12300 Pa + ½(1000)(3)2 + 0 = P2 + ½(1000)(0,75)2 + (1000)(9,8)(1,2)
P2 = 12300 Pa + ½(1000)(3)2 – ½(1000)(0,75)2 – (1000)(9,8)(1,2)
P2 = 4.080 Pa
Demikian pembahasan wacana aturan Bernoulli. Semoga bermanfaat. Baca juga Teori Kinetik Gas.