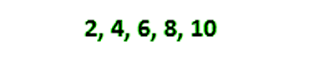Pengertian Definisi Arti : Metode statistik yaitu rumus, model, dan teknik matematika yang dipakai dalam analisis statistik data penelitian mentah. Penerapan metode statistik mengekstraksi informasi dari data observasi dan menawarkan berbagai cara untuk menilai kekokohan hasil observasi.
Statistik ialah cabang matematika yang berhubungan dengan pengumpulan, interpretasi, pengorganisasian, dan interpretasi data. Awalnya, dikala kita mendapatkan data, alih-alih menerapkan algoritma terbaik dan menciptakan beberapa prediksi, pertama-tama kita menjajal membaca dan mengetahui data dengan menerapkan teknik statistik. Dengan melakukan ini, kita dapat memahami jenis data distribusi apa yang dimiliki.
- STATISTIK DESKRIPTIF DAN STATISTIK INFERENSIAL
- PENGERTIAN DARI STATISTIK DESKRIPTIF
- APA JENIS STATISTIK DESKRIPTIF
- MENGUKUR TENDENSI PUSAT
- METODE PENGEMBILAN SAMPLE
- JENIS-JENIS DARI STATISTIK DESKRIPTIF
- PENGERTIAN DARI STATISTIK INFERENSIAL
- JENIS-JENIS DARI STATISTIK INFERENSIAL
- KESIMPULAN APA ITU METODE STATISTIKA DAN JENIS STATISTIK DESKRIPTIF
Daftar Isi
STATISTIK DESKRIPTIF DAN STATISTIK INFERENSIAL
Setiap siswa statistik harus tahu perihal banyak sekali cabang statistik untuk mengetahui statistik dengan benar dari sudut pandang yang lebih holistik. Seringkali, jenis pekerjaan atau observasi yang terlibat dalam menyembunyikan aspek statistik yang lain, namun sungguh penting untuk mengenali wangsit keseluruhan di balik analisis statistik untuk sepenuhnya menghargai kepentingan dan keindahannya.
Dua cabang utama statistik yaitu statistik deskriptif dan statistik inferensial. Keduanya digunakan dalam analisis data ilmiah dan keduanya sama pentingnya bagi siswa statistik.
Statistik deskriptif
Statistik deskriptif (deduktif) berhubungan dengan presentasi dan pengumpulan data. Ini umumnya merupakan bagian pertama dari analisis statistik. Dari kesimpulan pertimbangan para hebat beropini, Statistik Deskriptif (deduktif) atau sederhana adalah statistik yang tingkat pengerjaannya mencakup cara-cara menghitung, menyusun atau mengatur, mengolah, menghidangkan, dan menganalisa data biar mampu memberikan citra yang ringkas mengenai sebuah keadaan biasanya tidak sesederhana kedengarannya, dan hebat statistik perlu menyadari merancang eksperimen, memilih kelompok fokus yang sempurna dan menghindari bias yang begitu mudah untuk masuk ke dalam eksperimen.
Wilayah studi yang berlainan membutuhkan jenis analisis yang berlawanan memakai statistik deskriptif. Misalnya, seorang ahli fisika yang mempelajari turbulensi di laboratorium memerlukan jumlah rata-rata yang bervariasi dalam interval waktu yang kecil. Sifat dilema ini mensyaratkan bahwa jumlah fisik dirata-rata dari sejumlah data yang dikumpulkan lewat percobaan.
Statistik Inferensial
Statistik inferensial ialah mirip namanya, melibatkan penarikan kesimpulan yang sempurna dari analisis statistik yang sudah dikerjakan memakai statistik deskriptif. Pada kesannya, itu adalah kesimpulan yang membuat studi penting dan faktor ini ditangani dalam statistik inferensial.
Sebagian besar prediksi abad depan dan generalisasi tentang populasi dengan mempelajari sampel yang lebih kecil berada di bawah bidang statistik inferensial. Sebagian besar eksperimen ilmu sosial berurusan dengan mempelajari populasi sampel kecil yang membantu menentukan bagaimana populasi secara biasa bertingkah. Dengan mendesain eksperimen yang tepat, peneliti dapat menarik kesimpulan yang relevan dengan studinya.
Saat menggambar kesimpulan, seseorang mesti sangat waspada agar tidak menawan kesimpulan yang salah atau bias. Meskipun ini terlihat mirip suatu sains, ada cara di mana seseorang dapat memanipulasi studi dan hasil lewat banyak sekali cara. Sebagai contoh, pengerukan data kian menjadi problem alasannya adalah komputer menyimpan banyak isu dan mudah, baik secara sengaja atau tidak, memakai metode inferensial yang salah.
Statistik deskriptif dan inferensial berjalan beriringan dan satu tidak mampu ada tanpa yang lain. Metodologi ilmiah yang bagus perlu diikuti dalam kedua langkah analisis statistik ini dan kedua cabang statistik ini sama pentingnya bagi seorang peneliti.
PENGERTIAN DARI STATISTIK DESKRIPTIF
Statistik deskriptif melibatkan ringkasan dan pengorganisasian data sehingga gampang diketahui. Statistik deskriptif, tidak seperti statistik inferensial, berusaha menggambarkan data, namun jangan mencoba menciptakan kesimpulan dari sampel ke seluruh populasi. Di sini, kami biasanya menggambarkan data dalam sampel. Ini umumnya memiliki arti bahwa statistik deskriptif, tidak mirip statistik inferensial, tidak dikembangkan menurut teori probabilitas.
APA JENIS STATISTIK DESKRIPTIF
Statistik deskriptif dipecah menjadi dua kategori. Ukuran tendensi sentral dan ukuran variabilitas (penyebaran).
MENGUKUR TENDENSI PUSAT
Kecenderungan sentral mengacu pada gagasan bahwa ada satu angka yang paling baik merangkum seluruh rangkaian pengukuran, sebuah angka yang dalam beberapa cara “sentral” ke set.
Mean / rata-rata
Mari kita hitung rata-rata (mean) atau dikenal dengan average dengan kumpulan data yang mempunyai 8 bilangan lingkaran. Mean atau Rata-rata ialah kecenderungan sentral dari data ialah angka di mana seluruh data tersebar. Di satu segi, mean ialah angka tunggal yang mampu memperkirakan nilai seluruh kumpulan data.
Mari kita hitung mean dari kumpulan data yang mempunyai 8 bilangan bundar.
 |
| Gambar: Contoh perhitungan mean atau average |
Median
Median yakni nilai yang membagi data dalam 2 bab yang serupa ialah jumlah perumpamaan di segi kanan sama dengan jumlah perumpamaan di sisi kiri saat data disusun dalam urutan naik atau turun.
Catatan: Jika Kita mengurutkan data dalam urutan menurun, itu tidak akan memengaruhi median namun IQR akan negatif. Kita akan berbicara wacana IQR nanti di blog pengertianartidefinisidari.blogspot.com.
Median akan menjadi jangka menengah, jikalau jumlah istilahnya ganjil
Median akan menjadi rata-rata dari 2 perumpamaan tengah, jikalau jumlah istilahnya genap.
 |
| Gambar: Contoh perkiraan median |
Median adalah 59 yang hendak membagi set angka menjadi dua bagian yang sama. Karena ada angka genap dalam set, jawabannya yakni rata-rata angka tengah 51 dan 67.
Catatan: Ketika nilai berada dalam progresi aritmatika (perbedaan antara suku-suku berturut-turut ialah konstan. Ini 2.), median selalu sama dengan mean.
Rata-rata/ mean dari 5 angka ini adalah 6 dan lebih median.
Mode
Mode yaitu perumpamaan yang muncul waktu maksimum dalam kumpulan data adalah perumpamaan yang mempunyai frekuensi tertinggi.
 |
| Gambar: Contoh perhitungan mode |
Dalam kumpulan data ini, mode yaitu 67 sebab mempunyai lebih dari sisa nilai, misalnya dua kali.
Tetapi mungkin ada kumpulan data di mana tidak ada mode sama sekali alasannya adalah semua nilai timbul jumlah yang serupa kali. Jika dua nilai timbul waktu yang serupa dan lebih dari sisa nilai maka set data yaitu bimodal. Jika tiga nilai timbul waktu yang sama dan lebih dari sisa nilai maka set data adalah trimodal dan untuk mode n, set data tersebut multimodal.
METODE PENGEMBILAN SAMPLE
Untuk sebagian besar survei, sampel atau populasi target diperlukan, sebab populasinya terlalu besar untuk disurvei secara keseluruhan. Namun, jikalau populasinya cukup kecil, dimungkinkan untuk mensurvei setiap anggota. Jenis survei ini diketahui selaku studi sensus.
Dengan survei skala besar, sampel hampir senantiasa menjadi keperluan. Dua jenis utama sistem pengambilan sampel ialah probabilitas dan pengambilan sampel non-probabilitas.
Sampling Probabilitas
Metode sampling probabilitas didasarkan pada kemungkinan bahwa setiap anggota populasi memiliki kesempatan yang serupa untuk dipilih dalam sampel. Sebagian besar peneliti baiklah bahwa bentuk pengambilan sampel ini yakni yang paling dekat dengan yang mewakili populasi sebenarnya, karena bias insan dihilangkan dengan menggunakan pengacakan komputasi. Salah satu keuntungan utama dari sampling probabilitas yakni bahwa itu yang termudah untuk mengukur kesalahan. Metode pengambilan sampel probabilitas mencakup:
- Pengambilan sampel secara acak yakni bentuk yang paling benar dari probabilitas pengambilan sampel. Jenis pengambilan sampel ini menjamin bahwa setiap anggota populasi memiliki kesempatan yang sama untuk dimasukkan dalam sampel. Jenis pengambilan sampel ini ideal untuk studi yang lebih terkontrol di mana bias manusia dalam penyeleksian sampel tidak dapat ditoleransi.
- Stratified sampling ialah versi yang lebih mutakhir dari pengambilan sampel acak yang dimulai dengan memilih banyak sekali strata (yaitu, subset, pembagian) dalam sebuah populasi dan lalu menggambar secara acak dari setiap strata sehingga tidak mengecualikan atau salah menggambarkan satu strata. Contoh strata populer termasuk aneka macam etnis atau kalangan umur dalam sebuah populasi.
- Sampling sistematis, juga disebut teknik penyeleksian nama ke-n, sering dipakai sebagai pengganti pengambilan sampel acak alasannya prosesnya yang lebih sederhana. Setelah sampel dikumpulkan, setiap anggota ke-n dalam populasi dicatat dalam sampel. Misalnya, jikalau seorang mentor menginginkan sampel acak sistematis dari daftar penilaian yang didampingi, beliau mampu memilih setiap penilaian ke-7 dan menganalisis sampel yang diekstraksi ini selaku representasi yang lebih acak.
Kelemahan utama pengambilan sampel sistematis ialah bahwa contoh yang ditetapkan (mis., Setiap kali ke-7) mampu bertepatan dengan contoh fundamental lainnya dalam sampel. Sebagai pola, mentor mungkin memilih setiap evaluasi ke-7 secara acak, namun jika ia memiliki sesi pendampingan yang terpisah untuk setiap siswa yang ketujuh, dia akan memilih evaluasi pertama dari setiap sesi setiap kali dia memilih
- Pengambilan sampel multi-tahap intinya memadukan teknik dari beberapa metode pengambilan sampel
Sampling non-probabilitas
Sampling non-probabilitas sering dipakai dalam penelitian eksperimental atau percobaan yang lebih dan tidak menjamin representasi acak dan dekat dari populasi aktual. Alih-alih memakai pengacakan komputasi atau sistematis, pengambilan sampel non-probabilitas menggunakan evaluasi insan dan sering mengandalkan ketentraman semata. Beberapa dari aneka macam jenis pengambilan sampel non-probabilitas meliputi:
- Convenience sampling dipakai dikala para peneliti membutuhkan estimasi data yang efektif dari biaya yang mampu diperoleh dari melakukan sampling yang lebih acak. Biasanya, studi ini digunakan sebagai titik permulaan untuk studi yang lebih besar dan lebih komprehensif dengan sampel yang lebih representatif. Selain itu, seperti namanya, sampel yang dipilih ditarik terutama sebab tenteram.
- Sampling evaluasi sungguh bergantung pada penilaian insan untuk menentukan sampel yang merupakan representasi populasi yang tepat. Mirip dengan convenience sampling, judgment sampling bergantung pada evaluasi insan sering sebab sumber daya yang lebih efektif terlalu mahal atau tidak tersedia.
- Pengambilan sampel kuota dapat daripada pengambilan sampel bertingkat alasannya peneliti pertama kali mengidentifikasi aneka macam stratum dalam sebuah populasi. Berlawanan dengan pengambilan sampel bertingkat, pengambilan sampel kuota kemudian menggunakan sampel ketentraman atau evaluasi untuk menentukan anggota dalam setiap strata.
- Snowball sampling mempekerjakan anggota sampel saat ini untuk merekrut anggota embel-embel dalam populasi spesifik mereka dari ekspresi ke verbal. Setelah proses rekrutmen dimulai dan sampel anggota menandatangani studi, efeknya mirip dengan imbas bola salju. Pengambilan sampel bola salju sering digunakan dalam populasi yang unik atau tidak dapat didekati, yang sulit untuk dinilai secara menyeluruh kalau tidak.
JENIS-JENIS DARI STATISTIK DESKRIPTIF
Statistik deskriptif memungkinkan kita untuk mengkarakterisasi data kita menurut propertinya. Ada empat jenis utama statistik deskriptif:
- Ukuran Frekuensi:
- Hitung, Persen, Frekuensi
- Menunjukkan seberapa sering sesuatu terjadi
- Gunakan ini dikala Kita ingin menunjukkan seberapa sering respons diberikan
- Ukuran Tendensi Sentral
- Berarti, Median, dan Mode
- Menempatkan distribusi dengan aneka macam titik
- Gunakan ini dikala Kita ingin memperlihatkan bagaimana tanggapan rata-rata atau paling umum ditunjukkan
- Ukuran Dispersi atau Variasi
- Rentang, Varian, Deviasi Standar
- Mengidentifikasi sebaran skor dengan menyatakan interval
- Rentang = Tinggi / Rendah poin
- Varians atau Standar Deviasi = perbedaan antara skor yang diamati dan rata-rata
- Gunakan ini ketika Kita ingin menunjukkan seberapa “menyebar” data tersebut. Sangat membantu untuk mengenali kapan data Kita tersebar sedemikian sehingga memengaruhi rata-rata
- Ukuran Posisi
- Peringkat Persentil, Peringkat Kuartil
- Menjelaskan bagaimana skor jatuh dalam relasi satu sama lain. Bergantung pada skor tolok ukur
- Gunakan ini ketika Kita perlu membandingkan skor dengan skor yang dinormalisasi (misalnya., Norma nasional)
PENGERTIAN DARI STATISTIK INFERENSIAL
Statistik deskriptif menggambarkan data (contohnya, skema atau grafik) dan statistik inferensial memungkinkan kita membuat prediksi (“kesimpulan”) dari data itu. Dengan statistik inferensial, kita mengambil data dari sampel dan membuat generalisasi ihwal sebuah populasi. Misalnya, kita mungkin berdiri di mal dan meminta sampel 100 orang bila mereka suka membeli di pengertianartidefinisidari. Kita mampu menciptakan diagram batang jawaban ya atau tidak (yang akan menjadi statistik deskriptif) atau Kita mampu memakai observasi kita (dan statistik inferensial) untuk alasan bahwa sekitar 75-80% populasi (semua pembeli di semua mal) suka berbelanja di pengertianartidefinisidari.
JENIS-JENIS DARI STATISTIK INFERENSIAL
Statistik inferensial memungkinkan kita untuk menciptakan prediksi (“kesimpulan”). Ada dua jenis utama statistik inferensial:
- Memperkirakan parameter. Ini mempunyai arti mengambil statistik dari data sampel Kita (contohnya mean sampel) dan menggunakannya untuk mengatakan sesuatu ihwal parameter populasi (mis. Mean populasi).
- Tes hipotesis. Di sinilah Kita dapat memakai data sampel untuk menjawab pertanyaan penelitian. Misalnya, Kita mungkin kepincut mengenali apakah obat kanker gres efektif. Atau jika sarapan menolong belum dewasa tampil lebih baik di sekolah.
Katakanlah Kita memiliki beberapa sampel data tentang obat kanker gres yang potensial. Kita mampu menggunakan statistik deskriptif untuk menggambarkan sampel kita, tergolong:
- Rata-rata sampel
- Contoh persyaratan deviasi
- Membuat skema batang atau plot kotak
- Menjelaskan bentuk distribusi probabilitas sampel
Dengan statistik inferensial, Kita mengambil data sampel dari sejumlah kecil orang dan dan menjajal memilih apakah data tersebut dapat memprediksi apakah obat akan melakukan pekerjaan untuk siapa pun (yaitu populasi). Ada banyak sekali cara kita mampu melaksanakan ini, mulai dari menjumlah skor-z (skor-z ialah cara untuk menawarkan di mana data kita akan berada dalam distribusi normal sampai pengujian pasca-hoc (lanjutan).
Statistik inferensial memakai model statistik untuk membantu Kita membandingkan data sampel kita dengan sampel lain atau dengan observasi sebelumnya. Sebagian besar penelitian menggunakan model statistik yang disebut model Generalized Linear dan ANOVA (Analysis of Variance), analisis regresi dan berbagai model lainnya yang menghasilkan probabilitas dan hasil garis lurus (“linear”).
Prinsip utama untuk statistik inferensial ialah:
- Teorema Binomial
- Pengujian Hipotesis
- Distribusi Normal
- Distribusi-T
- Teorema Batas Pusat
- Interval Keyakinan
- Analisis Regresi / Regresi Linier
- Perbandingan Sarana.
KESIMPULAN APA ITU METODE STATISTIKA DAN JENIS STATISTIK DESKRIPTIF
Apa persamaan antara statistik deskriptif dan inferensial?
Statistik deskriptif dan inferensial bergantung pada set data yang serupa. Statistik deskriptif cuma mengandalkan kumpulan data ini, sementara statistik inferensial juga bergantung pada data ini untuk menciptakan generalisasi ihwal populasi yang lebih besar.
Apa kekuatan memakai statistik deskriptif untuk menilik distribusi skor?
Selain kejelasan statistik deskriptif yang dapat memperjelas volume data yang besar, tidak ada ketidakpastian tentang nilai yang Kita peroleh (selain cuma kesalahan pengukuran, dll.).
Apa keterbatasan statistik deskriptif?
Statistik deskriptif sungguh terbatas sehingga mereka cuma memungkinkan Kita untuk menciptakan penjumlahan wacana orang atau objek yang telah Kita ukur. Kita tidak mampu memakai data yang sudah Kita kumpulkan untuk digeneralisasi ke orang atau objek lain (mis., Menggunakan data dari sampel untuk menyimpulkan properti / parameter populasi). Misalnya, jika Kita menguji obat untuk mengalahkan kanker dan itu melakukan pekerjaan pada pasien Kita, Kita tidak mampu mengklaim bahwa itu akan melakukan pekerjaan pada pasien kanker lainnya hanya mengandalkan statistik deskriptif (namun statistik inferensial akan memberi Kita potensi ini).
Apa kekurangan statistik inferensial?
Ada dua batasan utama untuk penggunaan statistik inferensial. Keterbatasan pertama, dan yang paling penting, yang ada dalam semua statistik inferensial, ialah bahwa Kita menunjukkan data perihal populasi yang belum sepenuhnya diukur, dan oleh sebab itu, tidak pernah dapat sepenuhnya percaya bahwa nilai / statistik yang Kita hitung benar. Ingat, statistik inferensial didasarkan pada rancangan menggunakan nilai yang diukur dalam sampel untuk memperkirakan / menyimpulkan nilai yang hendak diukur dalam sebuah populasi; akan selalu ada tingkat ketidakpastian dalam melakukan ini. Batasan kedua terhubung dengan batas-batas pertama. Beberapa, namun tidak semua, tes inferensial mengharuskan pengguna (mis., Kita ) untuk menciptakan tebakan yang dididik (berdasarkan teori) untuk menjalankan tes inferensial. Sekali lagi, akan ada beberapa ketidakpastian dalam proses ini, yang hendak memiliki pengaruh pada kepastian hasil dari beberapa statistik inferensial.