Fungsi Kuadrat dan Grafiknya – Media Masyarakat

Daftar Isi

Pengertian fungsi kuadrat dan grafiknya

Fungsi kuadrat dan grafiknya adalah materi yang sudah mulai diajarkan di tingkat SMP, tetapi sebaiknya di review lagi ya..! Fungsi kuadrat yaitu fungsi yang variabel bebasnya paling tinggi berderajat dua. Bentuk umum fungsi kuadrat adalah :

$http://soulmath4u.blogspot.com/$

Dengan cara melengkapkan kuadrat sempurna akan didapat bentuk yang ekivalen dengan bentuk umumnya, yaitu :

$http://soulmath4u.blogspot.com/$

Dari bentuk (2) ini, nilai D = b²– 4ac disebut Diskriminan fungsi kuadrat, sehingga bentuk diatas dapat juga dituliskan sebagai berikut:

${\color{Red} y=a\left ( x+\frac{b}{2a} \right )^{2}-\frac{D}{4a}}\, ;\, dengan\,\,\, a\neq 0\, ....\, (3)$

Dari bentuk (3), maka :

Rumus persamaan sumbu simetri fungsi kuadrat adalah:

$x=-\frac{b}{2a}$
Rumus nilai ekstrem fungsi kuadrat, adalah:
$y=-\frac{D}{4a}$

Rumus titik ekstrem fungsi kuadrat, adalah:

$\left ( \frac{-b}{2a},\frac{-D}{4a} \right )$

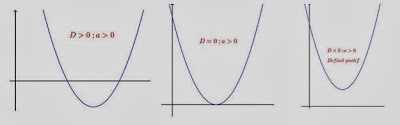
Sifat-sifat fungsi kuadrat dan grafiknya

Grafik fungsi kuadrat berbentuk parabola, dengan sifat-sifat seperti diabawah ini:

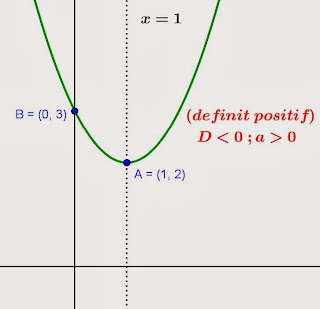
Jika a > 0, maka parabola akan terbuka keatas dan mempunyai nilai balik minimum
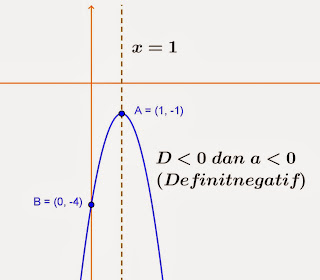
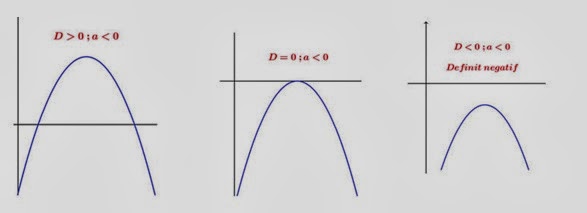
Jika a < 0, maka parabola akan terbuka kebawah dan mempunyai nilai balik maksimum
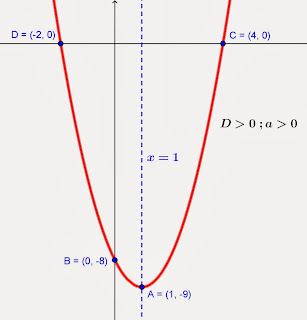
Jika D > 0, maka parabola akan memotong sumbu x pada dua titik
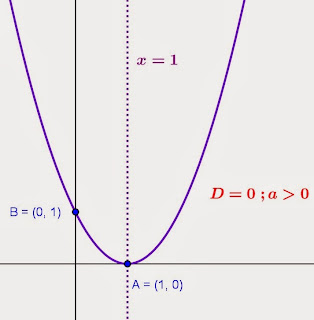
Jika D = 0, parabola memotong sumbu x hanya pada satu titik saja
Jika D < 0, parabola tidak memotong sumbu x.

Untuk lebih jelasnya tentang ilustrasi fungsi kuadrat dan grafiknya, perhatikan gambar dibawah ini:

Ada beberapa cara dalam menentukan titik puncak grafik fungsi kuadrat selain menggunakan rumus persamaan sumbu simetri dan rumus nilai ekstrem, yaitu dengan cara melengkapkan kuadrat sempurna. Dengan bentuk umumnya adalah:

$\begin{matrix} y=a\left ( x-h \right )^{2}+k\\\ast \, Sumbu\, simetri,\, x=h \\\ast \, Nilai\, ekstrem\, fungsi\, adalah,\, y=k \end{matrix}$

Selanjutnya setiap contoh-contoh yang disajikan dalam postingan ini penulis menggunakan cara melengkapkan kuadrat sempurna dalam mencari setiap titik puncak grafik fungsi kuadrat.

Dan teman-teman di asumsikan sudah menguasai cara melengkapkan kuadrat sempurna dengan baik sehingga lebih mudah dalam menyelesaikan soal-soal fungsi kuadrat dan grafiknya, tetapi jika belum dikuasai maka boleh menggunakan rumus-rumus yang telah diberikan diatas karena hasil akhirnyapun akan sama.

Contoh 1:

Tentukan Persamaan sumbu simetri, nilai minimum, dan titik puncak persamaan,
$y=x^{2}-2x+3$
[Penyelesaian]
$\begin{matrix} y=x^{2}-2x+3=\left ( x-1 \right )^{2}+2\\\therefore \, titik\, puncaknya\, ,\left ( 1,2 \right ) \end{matrix}$
$http://soulmath4u.blogspot.com/$

Contoh 2:

Tentukan Persamaan sumbu simetri, nilai minimum, dan titik puncak persamaan,
$y=-2x^{2}+4x-2$
[Penyelesaian]
$\\y=-2x^2+4x-2 \\y=-2(x^2-2x)-2 \\y=-2\left \{ (x-1)^2-1 \right \}-2 \\y=-2(x-1)^2 \\\\\therefore titik\, puncak\, (1,0) \\Persamaan \, sumbu\, simetri\, x=1 \\Nilai\, maksimum \, 0$

Langkah-langkah menyelesaikan soal-soal fungsi kuadrat dan grafiknya

Menentukan titik potong dengan sumbu x, untuk y = 0
Menentukan titik potong dengan sumbu y, untuk x = 0
Menentukan persamaan sumbu simetri, yaitu :
$x=-\frac{b}{2a}$
Menentukan nilai ekstrem , yaitu:
$y=\frac{-D}{4a}$
Menentukan titik ekstrem atau titik puncak, yaitu:
$\left ( \frac{-b}{2a} ,\frac{-D}{4a}\right )$
Menggambar sketsa grafik fungsi kuadrat.

Supaya lebih jelas tentang fungsi kuadrat dan grafiknya, coba teman-teman pelajari contoh-contoh dibawah ini.

Contoh 3:

Gambarlah grafik dari,
$y=x^{2}-2x-8$

[Penyelesaian]

Dengan mengikuti langkah-langkah menyelesaikan fungsi kuadrat dan grafiknya , yang telah dikemukakan diatas yaitu:
⬄ Menentukan titik potong dengan sumbu x, untuk y = 0 :
$\begin{matrix} x^{2}-2x-8=0\\ \left ( x-4 \right )\left ( x+2 \right )=0 \\ x=4\, atau\, x=-2 \\\therefore \, titik\, potong\, sumbu\, x\left ( 4,0 \right )dan\, \left ( -2,0 \right ) \end{matrix}$

⬄ Menentukan titik potong dengan sumbu y, untuk x = 0 :

$\begin{matrix} y=x^{2}-2x-8=0^{2}-2\times 0-8=-8\\\therefore titik\, potong\, sumbu\, y,\left ( 0,-8 \right ) \end{matrix}$

⬄ Menentukan titik puncak :
$\begin{matrix} y=x^{2}-2x-8\\y=\left ( x-1 \right )^{2}-1-8 \\ y=\left ( x-1 \right )^{2}-9 \\\therefore titik\, puncak\, A\left ( 1,-9 \right ) \end{matrix}$

⬄ Sketsa grafik:

Contoh 4:

Soal fungsi kuadrat dan grafiknya, dengan D > 0 dan a <0, Gambarlah grafik fungsi kuadrat ,

$y=-x^{2}+2x+3$

[Penyelesaian]

⬄ Titik potong dengan sumbu x, untuk y = 0,

⬄ Titik potong dengan sumbu y, untuk x = 0,
$y=-x^{2}+2x+3=-0^{2}+2\times 0+3=3 \\ \therefore \, titik\, potong\, sumbu\, y,B\left ( 0,3 \right )$

⬄ Menentukan titik puncak,
$\begin{matrix} y=-x^{2}+2x+3\Leftrightarrow y=-\left ( x^{2}-2x \right )+3\\\Leftrightarrow y=-\left \{ \left ( x-1 \right )^{2}-1 \right \} +3 \\\Leftrightarrow y=-\left ( x-1 \right )^{2} +4 \\\therefore titik\, puncak,\, A\left ( 1,4 \right ) \end{matrix}$
⬄ Sketsa grafik:

Contoh 5:

Pada contoh ini adalah fungsi kuadrat dan grafiknya, definit positif dengan a > 0 dan D < 0.

Gambarlah grafik fungsi kuadrat,
$y=x^{2}-2x+3$
[Penyelesaian]

⬄ Titik potong dengan sumbu x, untuk y = 0,
$\begin{matrix} y=x^{2}-2x+3\\D=b^{2}-4\times a\times c=2^{2}-4\times 1\times 3 =-8 \\karena\, D< 0,\, grafik\, tidak\, memotong\, sumbu\, x \\ \therefore tidak\, ada\, titik\, potong\, dengan\, sumbu\, x \end{matrix}$

⬄ Titik potong dengan sumbu y, untuk x = 0,
$\begin{matrix} y=x^{2}-2x+3=0^{2}-2\times 0+3=3\\ \therefore titik\, potong\, sumbu\, y,\, B\left ( 0,3 \right ) \end{matrix}$

⬄ Titik puncak grafik fungsi kuadrat,
Untuk menentukan titik puncak ubah terlebih dahulu persamaan kuadrat ke dalam bentuk:
$y=a\left ( x-h \right )^{2}+k$
dengan Cara melengkapkan kuadrat sempurna:

$\\y=x^2-2x+3 \\y=(x-1)^{2}-1+3 \\y=(x-1)^{2}+2 \\\\\therefore \,titik\,puncaknya\,\left ( 1,2 \right )$
⬄ Grafik Fungsi :

Contoh 6:

Contoh fungsi kuadrat dan grafiknya dengan D = 0, dan a > 0.

Gambarlah grafik fungsi kuadrat,
$y=x^{2}-2x+1$

[Penyelesain]

⬄ Titik potong dengan sumbu x, untuk y = 0,
$\\y=x^2-2x++1 \\x^2-2x+1=0 \\(x-1)^{2}=0 \\x=1 \therefore \,titik\,pot\, dengan\, sb\,x\,(1,0)$

⬄ Titik potong dengan sumbu y, untuk x = 0,
$\begin{matrix} y=x^{2}-2x+1=0^{2}-2\times 0+1=1\\\therefore titik\, potong\, sumbu\, y,B\left ( 0,1 \right ) \end{matrix}$ ,

⬄ Titik puncak grafik,

$http://soulmath4u.blogspot.com/$

⬄ Sketsa grafik :

Contoh 7

Contoh fungsi kuadrat dan grafiknya dengan D < 0, dan a < 0.

Gambarlah grafik fungsi kuadrat,
$y=-3x^{2}+6x-4$

[Penyelesaian]

⬄ Titik potong dengan sumbu x, untuk y = 0,
$\begin{matrix} y=-3x^{2}+6x-4\\D=b^{2}-4\times a\times c \\D=6^{2}-4\times \left ( -3 \right )\times \left ( -4 \right )=-12< 0 \\karena\, D< 0,\, grafik\, tidak\, memotong\, sumbu\, x \end{matrix}$

⬄ Titik potong dengan sumbu y, untuk x = 0,
$\begin{matrix} y=-3x^{2}+6x-4=0+0-4=4\\\therefore titik\, potong\, sumbu\, y,B\left ( 0,-4 \right ) \end{matrix}$

⬄ Titik puncak grafik,
$\begin{matrix} y=-3x^{2}+6x-4\Leftrightarrow y=-3\left ( x^{2}-2x \right )-4\\\Leftrightarrow y=-3\left \{ \left ( x-1 \right )^{2}-1 \right \}-4 \\\Leftrightarrow y=-3\left ( x-1 \right )^{2}-1 \\ \therefore titik\, puncaknya,\, A\left ( 1,-1 \right ) \end{matrix}$

⬄ Gambar grafik

Semoga bermanfaat, terimakasih sudah mengunjungi blog sederhana. Dan selamat berlatih menyelesaikan soal-soal fungsi kuadrat dan grafiknya.

materi yang masih berkaitan dengan materi ini Cara menentukan persamaan fungsi kuadrat

Kumpulan Soal Hubungan Parabola dan Garis