Fungsi Invers Matematika

by

Fungsi invers adalah konsep penting dalam matematika yang memiliki berbagai aplikasi dalam berbagai bidang, mulai dari ilmu komputer hingga ekonomi. Dalam artikel ini, kita akan menjelajahi apa itu fungsi invers, bagaimana cara menghitungnya, serta penerapannya dalam kehidupan sehari-hari.

I. Pengenalan Fungsi Invers

A. Apa itu Fungsi Invers?

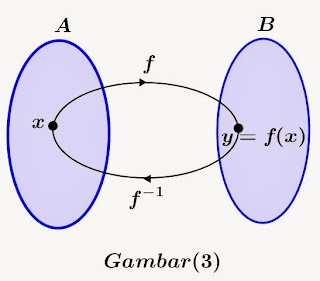
Fungsi invers adalah fungsi yang dapat membalikkan efek dari suatu fungsi lain. Dengan kata lain, jika sebuah fungsi mengubah input menjadi output, fungsi invers akan mengubah output tersebut kembali menjadi input asalnya. Misalnya, jika kita memiliki fungsi 𝑓(𝑥)f(x) yang mengubah suhu dalam Celsius menjadi Fahrenheit, fungsi inversnya akan mengubah Fahrenheit kembali menjadi Celsius.

B. Pentingnya Memahami Fungsi Invers

Memahami konsep fungsi invers penting karena memungkinkan kita untuk menyelesaikan berbagai masalah matematika dan menerapkannya dalam kehidupan sehari-hari. Dengan memahami bagaimana suatu fungsi dan inversnya saling berhubungan, kita dapat menemukan solusi untuk berbagai permasalahan yang melibatkan hubungan antara dua variabel.

II. Konsep Matematika Dasar

A. Definisi Fungsi

Sebelum memahami fungsi invers, penting untuk memiliki pemahaman yang kuat tentang fungsi dalam matematika. Secara sederhana, sebuah fungsi adalah aturan yang menghubungkan setiap elemen dalam domain dengan satu elemen dalam kodomain.

B. Konsep Fungsi Balik

Fungsi balik adalah fungsi yang mengubah output menjadi input. Dalam konteks fungsi invers, fungsi balik ini memainkan peran kunci dalam menemukan invers suatu fungsi.

III. Cara Menghitung Fungsi Invers

A. Langkah-langkah dalam Mencari Fungsi Invers

Untuk mencari fungsi invers suatu fungsi 𝑓(𝑥)f(x), langkah-langkah umumnya adalah sebagai berikut:

  1. Ganti 𝑓(𝑥)f(x) dengan 𝑦y.
  2. Tukar variabel 𝑥x dengan 𝑦y.
  3. Selesaikan persamaan untuk 𝑦y.
  4. Ganti 𝑦y dengan 𝑓−1(𝑥)f−1(x).

B. Contoh Penghitungan Fungsi Invers

Misalkan kita memiliki fungsi 𝑓(𝑥)=2𝑥+3f(x)=2x+3. Untuk mencari fungsi inversnya, kita dapat mengikuti langkah-langkah di atas untuk mendapatkan 𝑓−1(𝑥)f−1(x).

IV. Sifat-sifat Fungsi Invers

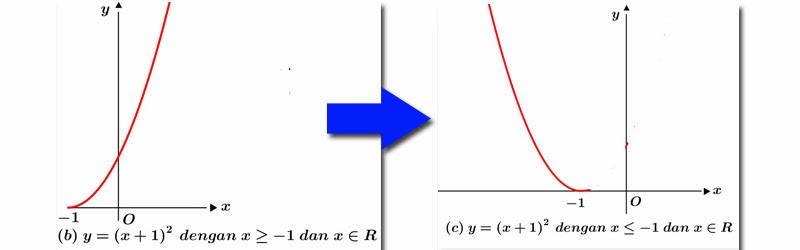
A. Simetri Terhadap Garis y = x

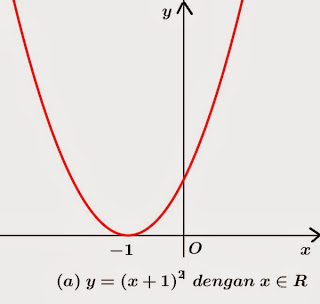
Fungsi invers memiliki sifat simetri terhadap garis 𝑦=𝑥y=x. Artinya, jika kita memplot fungsi 𝑓(𝑥)f(x) dan 𝑓−1(𝑥)f−1(x) pada grafik yang sama, keduanya akan mencerminkan satu sama lain melintasi garis 𝑦=𝑥y=x.

B. Komposisi Fungsi Invers

Komposisi dari suatu fungsi dengan inversnya akan menghasilkan nilai input yang sama dengan output aslinya. Dengan kata lain, 𝑓(𝑓−1(𝑥))=𝑥f(f−1(x))=x dan 𝑓−1(𝑓(𝑥))=𝑥f−1(f(x))=x.

V. Penerapan Fungsi Invers dalam Kehidupan Sehari-hari

A. Contoh-contoh Penerapan Fungsi Invers

Fungsi invers memiliki berbagai penerapan dalam kehidupan sehari-hari, seperti dalam:

  • Konversi satuan suhu
  • Kriptografi
  • Analisis ekonomi
  • Sistem navigasi GPS

VI. Kesimpulan

Fungsi invers adalah konsep matematika yang penting dan memiliki berbagai aplikasi dalam dunia nyata. Dengan memahami konsep ini, kita dapat memecahkan berbagai masalah matematika dan menerapkannya dalam berbagai bidang kehidupan.

  Sifat Operasi Penjumlahan Bilangan Bulat

Unique FAQs

  1. Apa perbedaan antara fungsi dan fungsi invers?
    • Fungsi mengubah input menjadi output, sedangkan fungsi invers mengubah output kembali menjadi input.
  2. Apa contoh penerapan fungsi invers dalam kehidupan sehari-hari?
    • Salah satu contohnya adalah dalam konversi satuan suhu, di mana kita dapat menggunakan fungsi invers untuk mengonversi suhu dari Celsius ke Fahrenheit dan sebaliknya.
  3. Mengapa penting untuk memahami fungsi invers?
    • Memahami fungsi invers penting karena memungkinkan kita untuk menyelesaikan berbagai masalah matematika dan menerapkannya dalam berbagai bidang kehidupan.
  4. Apakah semua fungsi memiliki invers?
    • Tidak, tidak semua fungsi memiliki invers. Fungsi harus memenuhi syarat tertentu untuk memiliki invers.
  5. Bagaimana cara menemukan invers suatu fungsi?
    • Salah satu cara umum adalah dengan mengikuti langkah-langkah yang telah ditentukan, yaitu mengganti 𝑓(𝑥)f(x) dengan 𝑦y dan menyelesaikan persamaan untuk 𝑦y.

Pengertian fungsi invers matematika

 
fungsi invers matematika merupakan materi yang berkaitan dengan fungsi jadi materi prasyarat dalam mempelajari materi ini adalah sudah terlebih dahulu menguasai berbagai macam bentuk fungsi seperti fungsi linier, fungsi kuadrat, fungsi irasional dan sebagainya.
Jadi, invers suatu fungsi f dapat didefinisikan sebagai berikut:
Jika fungsi  f : A —>B  dinyatakan dengan pasangan berurutan
Maka invers dari fungsi f adalah f-1 : B —>A ditentukan dengan
Catatan:
(1). Invers suatu fungsi belum tentu merupakan fungsi
(2). Jika invers suatu fungsi adalah fungsi maka invers fungsi tersebut disebut fungsi invers.
 
Untuk memperjelas catatan diatas perhatikan ilustrasi dalam diagram panah dibawah ini:
http://soulmath4u.blogspot.com/
 

 

http://soulmath4u.blogspot.com/

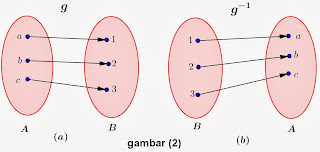
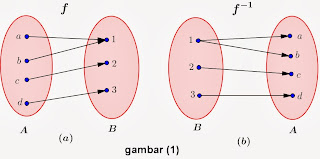
Perhatikan gambar (1.a) fungsi f merupakan pemetaan / fungsi, tetapi dari gambar (1.b) tampak bahwa f -1 merupakan relasi biasa ( bukan pemetaan / fungsi ), karena ada dua pasangan terurut yang mempunyai ordinat yang sama yaitu, (1,a) dan (1,b). Jadi, f -1 adalah invers fungsi bukan fungsi invers.

Sekarang perhatikan gambar (2.a), f merupakan pemetaan / fungsi. Dan dari gambar (2.b), f -1 juga merupakan fungsi. Jadi, f -1 adalah fungsi invers.
Sekarang kita sudah mendapatkan gambaran tentang definisi fungsi invers matematika, maka dari gambar (1) dan gambar (2) dapat ditarik kesimpilan bahwa:
Suatu fungsi f : A —> B mempunyai fungsi invers f -1 : B —->Ajika dan hanya jika f merupakan fungsi bijektif atau himpunan A dan B dalam korespondensi satu-satu.      (Sartono Wirodikromo, Matematika SMA. Jakarta : Erlangga).
 
  Tiga buah bilangan membentuk barisan aritmatika dengan beda tiga.
Cara menentukan rumus fungsi invers matematika
 
 
Jika f merupakan fungsi bijektif atau korespondensi satu-satu, maka invers dari fungsi f atau f -1 adalah fungsi invers. Coba perhatikan gambar (3) dibawah ini:
http://soulmath4u.blogspot.com/
Dari gambar (3), jika f merupakan fungsi bijektif dan y adalah bayangan (peta) dari x maka,
Jika f -1 adalah invers fungsi f , maka x adalah peta dari y oleh f  -1dapat dinyatakan dengan

Langkah-Langkah Menentukan Fungsi invers matematika 

 
 
Dari uraian diatas dapat diperoleh langkah-langkah menentukan fungsi invers matematika, yaitu sebagai berikut:
(1) Ubahlah persamaan bentuk y = f (x) dalam bentuk x sebagi fungsi y
(2) Bentuk x sebagai fungsi y pada langkah (1) di beri nama f -1 (y)
(3) Ubahlah y pada pada bentuk  f -1(y) dengan x untuk mendapatkan f -1 (x). f -1 (x) yang diperoleh adalah rumus fungsi invers dari f(x).
 
Supaya lebih memahami dan mampu menyelesaikan cara menentukan fungsi invers matematika, perhatikan contoh-contoh berikut ini:
 
Contoh 1 :
Tentukan rumus fungsi invers  dari  , y = 3 x + 6
[Penyelesaian]

y = 3 x + 6

Bentuk x sebagai fungsi dalam y,
 
Contoh 2 :
Tentukanlah rumus fungsi invers dari,  y = x3 – 1
[Penyelesaian]
Cara menentukan rumus fungsi invers matematika untuk soal diatas adalah, ubah terlebih dahulu ke bentuk x sebagai fungsi y  yaitu :

y = x3 – 1
Bentuk x sebagai fungsi dalam y,
 
Ada cara lain dalam menentukan rumus fungsi invers matematika suatu fungsi yaitu dengan menukar variabel nya.
 
Contoh 3 :
Tentukanlah rumus fungsi invers dari ,
[PenyelesaianG]
Tukarlah x dan y, maka
Susunlah kembali,
 
Contoh 4 :
Carilah rumus fungsi invers untuk,
[Penyelesaian]
 
Bentuk x sebagai fungsi dalam y,
 
Bagaimana menentukan rumus fungsi invers matematika jika fungsinya bukan merupakan fungsi bijektif? Maka harus diusahakan agar fungsi tersebut menjadi fungsi bijektif dengan cara membatasi domain alaminya. Perhatikan contoh soal dibawah ini!
 
Contoh 5 :
Diketahui fungsi f dengan rumus, f(x) = (x+1)2, tentukan rumus fungsi inversnya!
[Penyelesaian]
f(x) = (x+1)2 adalah fungsi kuadrat dengan domain f, Df = {x | x anggota R}, jika digambar grafiknya sebagai berikut :
http://soulmath4u.blogspot.com/
Dari grafik diatas , agar f(x) = (x+1)2 mempunyai invers maka domainya harus dibatasi yaitu,
 Perhatikan gambar dibawah ini untuk masing-masing domain:
http://soulmath4u.blogspot.com/
 
Perhatikan gambar (b) dan gambar (c) diatas, dengan membatasi domain alami dari fungsi f(x) = (x+1)2, maka fungsi tersebut menjadi fungsi bijektif. Maka cara menentukan fungsi invers matematika, f(x) = (x+1)2 adalah:
 
Seperti itulah cara menentukan fungsi invers matematika jika fungsinya bukan fungsi bijektif, yaitu dengan membatasi domain alaminya.
 
Contoh 6 :
Tentukan rumus fungsi invers jika,
[Penyelesaian]
 
Untuk contoh soal berikut ini, adalah bagaimana mencari fungsi f (x ), jika diketahui f -1(x ). Tentu caranya sama saja seperti menentukan fungsi invers matematika.
 
Contoh 7 :
Tentukan f (x), jika diketahui,
[Penyelesaian]
 
Dari contoh-contoh soal yang diberikan diatas anda diharapkan terampil dalam menyelesaikan soal-soal yang berkaitan dengan cara menentukan fungsi invers matematika.