Mari kita berguru tentang identitas trigonometri. Salah satu bahan dalam trigonometri ialah perbandingan sisi-sisi dalam segitiga. Pelajari lebih lanjut tentang Definisi Trigonometri.
Apakah kalian masih mengingatnya?
Perbandingan sisi segitiga tersebut digunakan untuk mempermudah dalam mengetahui sinus, cosinus, tangen, secan, cosecan, dan cotangen.
Dalam pembahasan kali ini akan dijelaskan perihal identitas trigonometri, grafik fungsi trigonometri, sudut-sudut istimewa dan pembahasan trigonometri yang lain.
Pelajari definisi identitas trigonometri berikut.
Daftar Isi
Definisi Identitas Trigonometri
Identitas trigonometri merupakan sebuah korelasi atau relasi antara suatu persamaan trigonometri dengan persamaan trigonometri yang lain.
Identitas trigonometri juga mencakup fungsi kebalikan, seperti
- Cosecan = 1/sin
- Secan = 1/cos
- Cotangen = 1/tan
begitu pulan sebaliknya. Masing-masing fungsi mampu digambarkan grafik fungsi trigonometrinya.
Pembahasan perihal grafik fungsi trigonometri akan diterangkan pada bagian berikutnya.
Pada bab di bawah ini akan dijelaskan pola penerapan identitas trigonometri.
Penerapan Identitas Trigonometri
Terdapat beberapa penerapan trigonometri dalam kehidupan sehari-hari misalnya bila kita ingin mengenali tinggi pohon, tiang bendera, atau tinggi gedung, maka kita cukup mengukur jarak gedung dengan titik contoh serta sudut elevasi permukaan tanah dengan puncak gedung.
Dengan langkah tersebut dan pengetahuan trigonometri yang kalian kuasai, maka akan dengan mudah mengkalkulasikan tinggi suatu objek.
Selanjutnya akan dibahas perihal grafik fungsi trigonometri.
Grafik Fungsi Trigonometri
Perhatikan beberapa grafik fungsi trigonometri berikut.
Grafik fungsi sinus
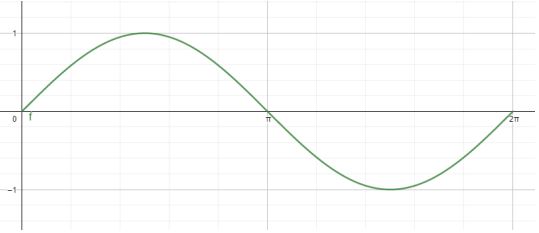
Grafik fungsi cosinus
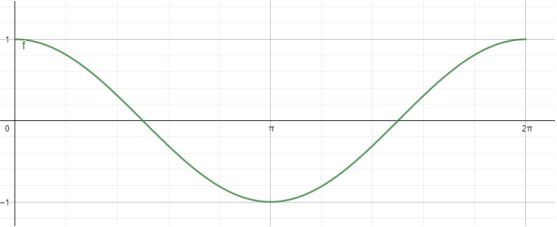
Grafik fungsi tangen
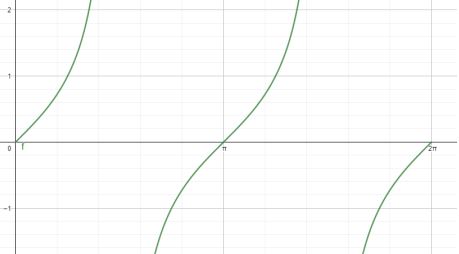
Beberapa grafik fungsi trigonometri tersebut dipakai untuk memudahkan dalam menentukan nilai sinus, cosinus, tangen, dan nilai trigonometri lainnya.
Berikut akan diterangkan perihal sudut istimewa.
Sudut Istimewa
Sudut-sudut istimewa merupakan beberapa sudut yang mampu dengan mudah kita tentukan nilai trigonometrinya.
Beberapa sudut istimewa tersebut adalah 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
Untuk nilai dari masing-masing sudut istimewa tersebut akan dijelaskan pada bab di bawah ini.
Tabel Trigonometri
Perhatikan grafik fungsi sinus berikut.

Pada grafik fungsi sinus tersebut, beberapa nilai sinusnya ialah
- sin 0° = 0
- sin 30° = ½
- sin 45° = ½ √2
- sin 60° = ½ √3
- sin 90° = 1
- sin 270° = -1
Perhatikan grafik fungsi cosinus berikut.

Beberapa niai cosinus dari fungsi tersebut yakni
- cos 0° = 1
- cos 30° = ½ √3
- cos 45° = ½ √2
- cos 60° = ½
- cos 90° = 0
Perhatikan grafik fungsi tangen berikut.

Beberapa nilai tangen dari fungsi tersebut adalah
- tan 0° = 0
- tan 30° = 1/√3
- tan 45° = 1
- tan 60° = √3
- tan 90° = (tidak terdefinisi)
Selanjutnya akan ditampilkan tabel sinus, cosinus, dan tangen.
Tabel Sin Cos Tan
Berikut merupakan tabel sinus, cosinus, dan tangen.
| α | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| sin α | 0 | ½ | ½ √2 | ½ √3 | 1 | ½ √3 | ½ √2 | 1/2 | 0 |
| cos α | 1 | ½ √3 | ½ √2 | ½ | 0 | -½ | -½ √2 | -½ √3 | -1 |
| tan α | 0 | 1/√3 | 1 | √3 | -√3 | -1 | -1/√3 | 0 |
| α | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin α | -1/2 | -½ √2 | -½ √3 | -1 | -½ √3 | -½ √2 | -½ | 0 |
| cos α | -½ √3 | -½ √2 | -½ | 0 | ½ | ½ √2 | ½ √3 | 1 |
| tan α | 1/√3 | 1 | √3 | -√3 | -1 | -1/√3 | 0 |
Keterangan:
α : besar sudut
Selanjutnya akan dijelaskan mengenai beberapa persamaan trigonometri.
Persamaan Trigonometri
Beberapa persamaan yang perlu kalian ketahui untuk mempermudah penyelesaian fungsi trigonometri yang lebih kompleks yakni
- sin (90° – x) = cos x
- sin (90° + x) = cos x
- sin (180° – x) = sin x
- sin (180° + x) = – sin x
- cos (90° – x) = sin x
- cos (90° + x) = – sin x
- cos (180° – x) = – cos x
- cos (180° + x) = – cos x
Beberapa persamaan trigonometri berikut ialah bentuk identitas trigonometri.
Identitas trigonometri kepada sinus
- sin 2x = 2 sin x cos x
- sin (a + b) = sin a cos b + cos a sin b
- sin (a – b) = sin a cos b – cos a sin b
- sin2 x = 1 – cos2x
Identitas trigonometri terhadap cosinus
- cos 2x = cos2x – sin2x
- cos 2x = 2 cos2x – 1
- cos 2x = 1 – 2 sin2x
- cos2x = 1- sin2x
- cos (a + b) = cos a cos b – sin a sin b
- cos (a – b) = cos a cos b + sin a sin b
Identitas trigonometri yang lain
- sec2x – tan2x = 1
- sin2x + cos2x = 1
Keterangan:
x, a, b : besar sudut
Coba lakukan soal di bawah ini selaku latihan.
Contoh Soal Grafik Fungsi Trigonometri
1. Tentukan nilai dari
- sin 120°
- cos 225°
- tan 60°
- sin 270°
- cos 90°
- tan 180°
- sin 120° = ½ √3
- cos 225° = – ½ √2
- tan 60° = √3
- sin 270° = -1
- cos 90° = 0
- tan 180° = 0
2. Tentukan nilai fungsi trigonometri berikut.
- sin 105°
- cos 15°
- sin270° + cos270°
sin 105° = sin (60° + 45°)
sin (60° + 45°) = sin 60° cos 45° + cos 60° sin 45°
= ½ √3 . ½ √2 + ½ . ½ √2
= ¼ √6 + ¼ √2 = ¼ (√6 + √2)
cos 15° = cos (45° – 30°)
cos (45° – 30°) = cos 45° cos 30° + sin 45° sin30°
= ½ √2 . ½ √3 + ½ √2 . ½
= ¼ √6 + ¼ √2 = ¼ (√6 + √2)
sin270° + cos270°
Karena sin2x + cos2x = 1, maka sin270° + cos270° = 1
Mari kita simpulkan bersama.
Kesimpulan
- Identitas trigonometri merupakan sebuah kekerabatan atau korelasi antara sebuah persamaan trigonometri dengan persamaan trigonometri yang lain.
- Beberapa sudut istimewa yakni 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
- Untuk menentukan besar sinus, cosinus, dan tangen sudut dapat dengan melihat nilai pada grafik fungsi trigonometri.
- Besar sinus, cosinus, dan tangen dari sudut istimewa
| α | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| sin α | 0 | ½ | ½ √2 | ½ √3 | 1 | ½ √3 | ½ √2 | 1/2 | 0 |
| cos α | 1 | ½ √3 | ½ √2 | ½ | 0 | -½ | -½ √2 | -½ √3 | -1 |
| tan α | 0 | 1/√3 | 1 | √3 | -√3 | -1 | -1/√3 | 0 |
| α | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin α | -1/2 | -½ √2 | -½ √3 | -1 | -½ √3 | -½ √2 | -½ | 0 |
| cos α | -½ √3 | -½ √2 | -½ | 0 | ½ | ½ √2 | ½ √3 | 1 |
| tan α | 1/√3 | 1 | √3 | -√3 | -1 | -1/√3 | 0 |
- Beberapa bentuk identitas fungsi trigonometri ialah:
sin 2x = 2 sin x cos x
cos 2x = cos2x – sin2x = 2 cos2x – 1 = 1 – 2 sin2x
sin2x + cos2x = 1
Demikian pembahasan tentang identitas trigonometri kali ini. Semoga mampu menambah pengetahuan kalian ihwal matematika, khusunya perihal trigonometri. Baca juga Limit Trigonometri.