Pada kesempatan kali ini, kita akan mempelajari salah satu bentuk bilangan ialah kepingan. Simak klarifikasi di bawah mengenai potongan.
Pernahkah kalian mengetahui tentang penjabaran/pengelompokan bilangan? Dalam pengelompokan bilangan terdapat bilangan rasional/belahan.
Seperti apakah bilangan cuilan itu?
Perhatikan penjelasan berikut.
Daftar Isi
Bilangan Pecahan
Bilangan pecahan merupakan salah satu kelompok bilangan dengan bentuk a/b dimana a dan b merupakan bilangan lingkaran serta b tidak sama dengan nol. Nilai a dan b saling prima, artinya tidak ada faktor/pembagi yang mampu membagi a dan b sekaligus.
Dalam bilangan cuilan, a disebut selaku pembilang sedangkan b disebut sebagai penyebut cuilan.
Penerapan Bilangan Pecahan
Penerapan bilangan bagian lazimnya dipakai untuk menyatakan bilangan yang tidak bulat.
Bentuk penggalan (cuilan lazimmaupun desimal) sangat sempurna untuk menunjukkan sebuah nilai yang tidak bulat.
Bilangan cuilan dapat dipakai sebagai representasi perbandingan sebuah bab terhadap keseluruhan.
Selanjutnya akan diterangkan mengenai cuilan biasa.
Pecahan Biasa
Pecahan umumatau mampu disebut sebagai cuilan merupakan bentuk cuilan yang kita lihat umumnya. Pecahan umumberbentuk a/b dengan a ialah pembilang dan b merupakan penyebut. Contohnya sebagai berikut.
4/5 ialah sebuah potongan umumdengan 4 selaku pembilang dan 5 selaku penyebut.
1/7 meruapakan sebuah bagian biasa dengan 1 sebagai pembilang dan 7 sebagai penyebut.
Selanjutnya akan dibahas tentang belahan adonan.
Pecahan Campuran
Pecahan adonan ialah jenis bilangan potongan yang berisikan bab lingkaran dan bab potongan. Pecahan gabungan dapat berupa c a/b dengan c ialah bilangan bundar dan a/b ialah bagian cuilan.
Contoh belahan campuran yaitu 3 2/5 dengan 3 ialah bagian bundar dan 2/5 merupakan bab pecahannya.
Cara mengubah serpihan adonan menjadi potongan biasa ialah dengan mengalikan bagian lingkaran dengan penyebut bagian belahan lalu menjumlahkannya dengan bagian pembilang dari penggalan.
Misalnya terdapat cuilan 2 4/5, kalau diubah menjadi bagian biasa menjadi (2 x 5 + 4)/5 sehingga menjadi 14/5.
Selanjutnya merupakan pembahasan perihal kepingan desimal.
Pecahan Desimal
Pecahan desimal merupakan salah satu bentuk nilai penggalan dengan penyebut 10, 100, 1000, dan seterusnya. Penulisan bilangan pecahan desimal dengan menggunakan tanda koma “ , “. Beberapa acuan berikut ialah bentuk penggalan desimal.
- Bilangan persepuluhan misalnya 3/10 ditulis dengan 0,3.
- Bilangan perseratusan misalnya 21/100 ditulis dengan 0,21.
- Bilangan perseribuan misalnya 197/1000 ditulis dengan 0,197.
Selanjutnya akan dibahas mengenai serpihan senilai.
Pecahan Senilai
Apakah yang dimaksud dengan kepingan senilai? Pecahan senilai mampu diartikan selaku dua atau lebih serpihan dengan perbandingan nilai pembilang dan penyebutnya sama. Perhatikan acuan di bawah ini biar lebih memahaminya.
Misalnya terdapat kepingan 2/5, 4/10, dan 10/25. Ketiga cuilan tersebut merupakan kepingan senilai.
- 2/5, perbandingan pembilang dan penyebutnya yaitu 2 : 5.
- 4/10, perbandingan pembilang dan penyebutnya adalah 4 : 10 = 2 : 5.
- 10/25, perbandingan pembilang dan penyebutnya yakni 10 : 25 = 2 : 5.
Karena ketiga cuilan tersebut memiliki perbandingan pembilang dan penyebut yang serupa, maka ketiga serpihan tersebut ialah penggalan yang senilai.
Selanjutnya akan dibahas perihal bagaimana cara mempersempit pecahan.
Menyederhanakan Pecahan
Bagaimana cara menyederhanakan kepingan?
Menyederhanakan pecahan dapat dilakukan dengan membagi pembilang dan penyebut dengan faktor pembagi paling besar dari keduanya. Misalnya terdapat penggalan 24/32.
Pembagi terbesar dari kedua bilangan 24 dan 32 ialah 8, sehingga belahan paling sederhana dari 24/32 ial
ah (24 : 8)/(32 : 8) = 3/4.
Pada bab berikut ini akan dibahas mengenai pertidaksamaan penggalan.
Pertidaksamaan Pecahan
Pertidaksamaan cuilan melibatkan tanda kurang dari “ < “ atau lebih dari “ > “. Kedua tanda tersebut digunakan untuk membandingkan dua nilai penggalan.
Perhatikan klarifikasi berikut.
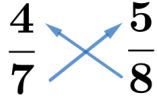
Terdapat cuilan 4/7 dan 5/8. Untuk membandingkan kedua pecahan tersebut dapat dikerjakan dengan mengalikan pembilang cuilan pertama dengan penyebut pecahan kedua dan sebaliknya. Sehingga (4 x 8) …….. (5 x 7) à 32 …… 35.
Tanda yang tepat untuk pertidaksamaan serpihan tersebut yaitu kurang dari “ <”
Kaprikornus, (4/7) < (5/8).
Selanjutnya ialah penjelasan perihal pengurutan potongan. Baca juga Bilangan cacah.
Mengurutkan Pecahan
Pada bagian ini akan dibahas mengenai mengurutkan belahan dengan bentuk yang sama dan berlawanan.
Mengurutkan serpihan dengan penyebut yang serupa.
Misalkan terdapat beberapa pecahan ialah 2/7; 3/7; 6/7; 1/7; dan 5/7. Mengurutkan serpihan dengan bentuk tersebut dapat dikerjakan dengan mengamati pembilangnya (alasannya penyebutnya memiliki nilai yang sama). Sehingga urutan pecahan dari yang terkecil ialah 1/7; 2/7; 3/7; 5/7; 6/7.
Mengurutkan bagian dengan penyebut yang berbeda.
Misalkan terdapat potongan 2/3; 1/2; 3/4. Mengurutkan bagian tersebut mampu dilakukan dengan menyamakan penyebutnya. Pecahan-belahan tersebut mampu disamakan penyebutnya menjadi 8/12; 6/12; 9/12. Sehingga kita mampu mengurutkannya dengan mudah adalah menyaksikan nilai pembilangnya 6/12; 8/12; 9/12 à 1/2; 2/3; 3/4.
Selain memakai cara tersebut, kalian mampu menggunakan cara dengan membandingkan masing-masing pecahan menggunakan desain pertidaksamaan kepingan yang sudah kalian pelajari pada bagian sebelumnya.
Mengurutkan penggalan dengan jenis yang berlawanan.
Misalkan terdapat penggalan 3/10; 0,35; 32%; 31/100. Mengurutkan cuilan tersebut dengan menggantinya ke dalam bentuk yang serupa. Misalkan kita akan menggantinya ke dalam bentuk serpihan desimal, diperoleh:
3/10 = 0,3 = 0,30
0,35
32% = 32/100 = 0,32
31/100 = 0,31
Jika diurutkan akan menjadi 0,30; 0,31; 0,32; 0,35 à 3/10; 31/100; 32%; 0,35.
Kerjakan soal potongan berikut untuk meningkatkan kemampuan matematika kalian. Baca juga Bilangan Bulat.
Soal Pecahan
1. Ubahlah pecahan biasa berikut menjadi potongan adonan.
- 30/7
- 14/3
- 27/5
30/7 = (28 + 2)/7 = 4 2/7.
14/3 = (12 + 2)/3 = 4 2/3.
27/5 = (25 + 2)/5 = 5 2/5.
2. Sederhanakan bagian-penggalan berikut.
- 28/42
- 32/48
- 17/51
28/42 = (28 : 14)/(42 : 14) = 2/3
32/48 = (32 : 16)/(48 : 16) = 2/3
17/51 = (17 : 17)/(51 : 17) = 1/3
3. Tanda pertidaksamaan yang tepat untuk (4/9) …. (2/5) yakni . . . .
(4/9) …. (2/5) à (4 x 5) . . . (2 x 9) à 20 > 18.
Tanda pertidaksamaan yang tepat yaitu >.
4. Urutkan belahan berikut dari yang terbesar.
2/3; 3/4; 2/5; 7/12.
Jawaban: 3/4; 2/3; 7/12; 2/5.
2/3 = (2 x 20)/(3 x 20) = 40/60
3/4 = (3 x 15)/(4 x 15) = 45/60
2/5 = (2 x 12)/(5 x 12) = 24/60
7/12 = (7 x 5)/(12 x 5) = 35/60
Sehingga urutannya dari yang terbesar yakni 3/4; 2/3; 7/12; 2/5.
Mari kita simpulkan bersama.
Kesimpulan
- Bilangan penggalan merupakan salah satu kelompok bilangan dengan bentuk a/b dimana a dan b merupakan bilangan lingkaran serta b tidak sama dengan nol.
- Terdapat berbagai macam serpihan mirip penggalan biasa, cuilan adonan, dan cuilan desimal.
- Menyederhanakan bagian mampu dijalankan dengan membaginya menggunakan bilangan paling besar yang membagi pembilang dan penyebut sekaligus.
- Pertidaksamaan potongan yaitu membandingkan dua nilai serpihan. Caranya dengan mengalikan pembilang potongan pertama dengan penyebut serpihan kedua dan juga sebaliknya.
- Mengurutkan pecahan mampu dikerjakan dengan mengubahnya ke dalam bentuk serpihan yang sama.
Demikian penjelasan mengenai materi kepingan. Semoga banyak menunjukkan manfaat terhadap pembaca sekalian. Terima kasih. Pelajari juga Bilangan Prima.