Pernahkah kalian mendengar KPK dan FPB?
Kali ini, kita akan membicarakan mengenai KPK dan FPB. Jadi, mari kita simak materinya semoga kita lebih paham ihwal KPK dan FPB.
Daftar Isi
Pengertian KPK
Kelipatan komplotan terkecil atau yang disingkat KPK dalam bahasa inggris diketahui selaku least common multiple (LCM).
KPK dari 2 atau lebih bilangan merupakan bilangan yang ialah kelipatan komplotan terkecil dari 2 atau lebih bilangan tersebut.
Dengan kata lain, KPK dari 2 atau lebih bilangan yaitu bilangan lingkaran positif terkecil yang dapat dibagi dengan 2 atau lebih bilangan tersebut.
Cara Mencari Nilai KPK
Dalam mencari nilai KPK terdapat 2 tata cara yang dapat dipakai, yakni
1. Metode sederhana
Misal kita akan mencari KPK dari 14 dan 4, maka cara mencari KPK menggunakan sistem sederhana yaitu
Kelipatan 14 = 14, 28, 42, 56, 70, …
Kelipatan 4 = 4, 8, 12, 16, 20, 24, 28, 32, …
KPK dari 14 dan 4 adalah kelipatan yang sama dan terkecil, jadi KPK nya yaitu 28
2. Metode faktorial
Metode ini menggunakan pohon faktorial. Misalkan kita akan mencari KPK dari 20 dan 45 maka cara mencari KPK nya yaitu
Buat pohon faktornya

susun bilangan dari pohon aspek sehingga ditemukan faktorialnya
- faktorial 20 = 22 x 51
- faktorial 45 = 32 x 51
ambil faktor yang memiliki pangkat paling besar yakni 22 x 32 x 51
kalikan aspek faktor tersebut 4 x 9 x 5 = 180
Kaprikornus, KPK dari 20 dan 45 yaitu 180.
Baca juga Fungsi Kuadrat.
Pengertian FPB
Faktor komplotan terbesar atau yang disingkat FPB dalam bahasa inggris diketahui sebagai Great common divisor (GCD).
FPB dari 2 atau lebih bilangan ialah bilangan lingkaran aktual paling besar yang dapat membagi habis kedua (atau lebih) bilangan tersebut.
Cara Mencari Nilai FPB
Hampir sama seperti KPK, dalam mencari nilai FPB terdapat 2 tata cara yang dapat dipakai, ialah
1. Metode sederhana
Misal kita akan mencari FPB dari 14 dan 4, maka cara mencari KPK menggunakan sistem sederhana yakni
Faktor 14 = 1, 2, 7, 14
Faktor 4 = 1, 2, 4
FPB dari 14 dan 4 yakni aspek yang serupa dan terbesar, jadi FPB nya yakni 2
2. Metode faktorial
Metode faktorial memiliki 2 alternatif cara yakni menggunakan pohon aspek.
Misalkan kita akan mencari FPB dari 20 dan 30 maka cara mencari FPB nya adalah
Buat pohon faktornya
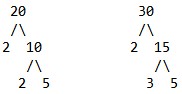
susun bilangan dari pohon faktor sehingga didapatkan faktoria
lnya
- faktorial 20 = 22 x 51
- faktorial 30 = 21 x 31 x 51
ambil faktor yang serupa ialah 2 dan 5
kalikan aspek yang sama dan memiliki pangkat terkecil adalah 21 x 51
kalikan aspek aspek tersebut 2 x 5 = 10
Kaprikornus, FPB dari 20 dan 30 yaitu 10.
Baca juga Sudut.
Contoh Soal KPK dan FPB
1. Terdapat 2 motor di rumah Ani yang harus secara berkala di servis ke bengkel. Motor pertama mesti di servis setiap 30 hari sekali, sedangkan motor satunya harus diservis setiap 25 hari sekali. Setiap berapa hari kah Ani mesti menjinjing kedua motornya untuk diservis tolong-menolong?
Akan dicari KPK dari 25 dan 30 memakai pohon faktorial
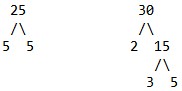
Faktorial 25 = 52
Faktorial 30 = 2 x 3 x 5
Diperoleh KPK dari 25 dan 30 yaitu 2 x 3 x 52 = 150
Jadi, setiap 150 hari Ani akan membawa kedua motornya untuk diservis bersama-sama.
2. Andi memiliki 15 roti coklat dan 20 roti pisang. Roti tersebut akan dimasukkan kedalam kantong plastik dengan komposisi yang sama untuk dibagikan kepada temannya. Berapa kantong berisi roti yang dapat dibuat Andi?
Akan dicari FPB dari 15 dan 20 menggunakan tata cara sederhana
- Faktor 15 = 1, 3, 5, 15
- Faktor 20 = 1, 2, 4, 5, 10, 20
- FPB dari 14 dan 4 yaitu faktor yang serupa dan paling besar, maka FPB nya yaitu 5
Makara, jumlah kantong plastik yang berisi roti dengan komposisi yang serupa adalah 5 kantong plastik
Demikian pembahasan tentang KPK dan FPB, biar berfaedah. Baca juga Kalkulus.