Soal Statistika

Soal Statistika – Ini memang kami sampikan untuk anda semua alasannya di situs kunci jawaban akan memperlihatkan pembahasan lengkap bukan cuma materi Soal Statistika ini saja namun aneka macam dari soal Umum, Soal SD, Soal MI, Soal Sekolah Menengah Pertama, Soal MTs, Soal Sekolah Menengan Atas MA, Soal SMK, Hingga Perguruan Tinggi. Tentunya dengan hal ini situs ini akan menawarkan kelengkapan untuk anda mampu belajari pribadi untuk materi teladan Soal tersebut.

Untuk Postingan kali ini kami bagikan secara langsung tentang pembahasan Soal Statistika sehingga dengan Soal Statistika ini maka anda bisa langsung pelajari soal soal tersebut. Oya untuk situs kunci tanggapan juga memberikan Bank Soal yang ada di positingan ini dimana semua postingan dan materi soal yang kami update setiap hari mampu dilihat di artikel Bank Soal yang suda ada di sidebar dan header dari situ ini.

Anda mampu menyaksikan semua soal-soal tersebut lengkap tinggal pilih materi soal yang anda ingin pelajari. Karena untuk Bank Soal tersebut yakni mencakum semua isi konten di situs kunci jawaban.

Tidak usa usang-lama maka dapatkan Soal Statistika yang kami posting dibawah ini biar bisa bermainfaat buat anda semua yang ketika ini ingin memelajari Soal Statistika ini.

Contoh 1: Nilai Rata-rata

Diketahui data selaku berikut : 7, 8, 8, 9, 7, 6, 5, 8. Nilai rata-rata dari data tersebut adalah ….
A. 8,25
B. 7,25
C. 6,50
D. 6,00

Pembahasan :
Nilai rata-rata ialah hasil bagi jumlah data dengan banyak data.

⇒ x =	7 + 8 + 8 + 9 + 7 + 6 + 5 + 8
	8

⇒ x = 58/8
⇒ x = 7,25

Contoh 2: Rata-rata Gabungan
Nilai rata-rata Fisika dari 10 murid pria ialah 7,50 sedangkan nilai rata-rata dari 5 murid wanita yaitu 7,00. Jika nilai mereka digabungkan, maka nilai rata-ratanya menjadi …
A. 7,75
B. 7,45
C. 7,33
D. 7,25

Pembahasan :
Dari soal dikenali:
1). Jumlah murid pria : n_L = 10 orang
2). Jumlah murid perempuan : n_p = 5 orang
3). Nilai rata-rata pria : x_L = 7,50
4). Nilai rata-rata perempuan : x_p = 7,00

Nilai rata-rata gabungan:

⇒ xg =	nL.xL + np.xp
	nL + np

⇒ xg =	10(7,50) + 5(7,00)
	10 + 5

⇒ xg =	75 + 35
	15

⇒ x_g = 110/15
⇒ x_g = 7,33

Contoh 3: Penyajia Data dan Menentukan Modus Data

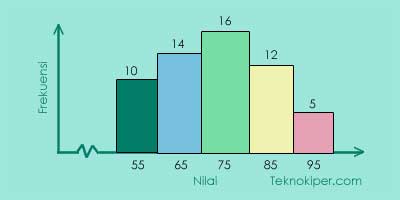
Perhatikan gambar di bawah ini!

Berdasarkan distribusi frekuensi yang ditunjukkan oleh diagram di atas, modus data tersebut adalah …
A. 75,25
B. 75,00
C. 70,65
D. 70,25

Pembahasan :
Modus yakni data yang paling kerap timbul. Dengan kata lain, modus adalah data yang mempunyai frekuensi terbesar. Dari gambar di atas, nilai yang paling sering muncul (frekuensinya terbesar kotaknya paling tinggi) ialah 75.

Contoh 4: Rata-rata Gabungan
Nilai rata-rata dari 14 murid untuk ujian kimia yaitu 66,25 sebelum ditambah dengan nilai Andi. Setelah nilai ujian Andi keluar, ternyata nilai rata-ratanya menjadi 65,50. Nilai cobaan Andi ialah …
A. 67,50
B. 65,25
C. 60,55
D. 55,00

Pembahasan :
Dari soal diketahui:
1). Jumlah murid kelompok pertama : n₁ = 14 orang
2). Jumlah murid golongan kedua : n₂ = 1 orang
3). Nilai rata-rata pertama : x₁ = 66,25
4). Nilai rata-rata adonan : x_g = 65,50

Nilai Andi sama dengan nilai rata-rata golongan kedua karena pada kelompok kedua cuma ada satu murid adalah Andi. Dengan demikian, nilai Andi dapat dihitung dengan rumus rata-rata adonan:

⇒ xg =	n1.x1 + n2.x2
	n1 + n2

⇒ 65,50 =	14(66,25) + 1 .x2
	14 + 1

⇒ 65,50 =	927,5 + x2
	15

⇒ 65,50 x 15 = 927,5 + x₂
⇒ 982,5 = 927,5 + x₂
⇒ x₂ = 982,5 – 927,5
⇒ x₂ = 55
⇒ Nilai Andi = x₂ = 55

Contoh 5: Menentukan Median Data

Median dari data : 5, 6, 6, 8, 7, 6, 8, 7, 6, 9 adalah …
A. Me = 6
B. Me = 6,25
C. Me = 6,5
D. Me = 7

Pembahasan :
Median adalah nilai tengah dari data. Untuk menentukan median, datanya harus diurutkan terlebih dulu. Urutan data : 5, 6, 6, 6, 6, 7, 7, 8, 8, 9

Median dari data di atas ialah:

⇒ Me =	6 + 7
	2

⇒ Me = 13/2
⇒ Me = 6,5

Contoh 6: Menenetukan Median Data Berdasarkan Tabel
Perhatikan data pada tabel berikut!

Nilai	60	65	70	75	80	85	90	95
Frekuensi	1	4	2	10	11	3	1	1

Median dari data di atas yaitu …
A. 75
B. 75,5
C. 80
D. 85

Pembahasan :
Langkah pertama kita hitung banyak datanya lalu kita pastikan letak median datanya menurut rumus.

Banyak data:
⇒ n = ∑Frekuensi
⇒ n = 1 + 4 + 2 + 10 + 11 + 3 + 1 + 1
⇒ n = 33

Letak median:

⇒ Letak Me =	n + 1
	2

⇒ Letak Me =	33 + 1
	2

⇒ Letak Me = 34/2
⇒ Letak Me = 17

Kaprikornus, median datanya terletak pada data ke-17. Berdasarkan tabel, data ke-17 berada kolom nilai ke-4, dengan nilai 75. Jadi, median datanya adalah 75.

Contoh 7: Menentukan Modus Data

Modus untuk data pada tabel nomor 6 di atas adalah …
A. 80
B. 75,5
C. 75
D. 70

Pembahasan :
Modus adalah data yang mempunyai frekuensi tertinggi. Pada tabel di atas, frekuensi tertinggi yakni 11 dan nilai yang timbul sebanyak 11 kali yaitu 80.

Contoh 8: Perbandingan Banyak Data
Nilai rata-rata cobaan Matematika di kelas X-A yakni 65. Jika nilai rata-rata untuk murid laki-laki adalah 63 dan nilai rata-rata untuk murid wanita ialah 70, maka perbandingan banyak murid pria dan murid perempuan di kelas itu ialah …
A. 5 : 4
B. 5 : 3
C. 5 : 2
D. 2 : 5

Pembahasan :
Dari soal dikenali :
1). Jumlah murid golongan pertama : n_L = 14 orang
2). Jumlah murid golongan kedua : n_P = 1 orang
3). Nilai rata-rata murid laki-laki : x_L = 63
3). Nilai rata-rata murid laki-laki : x_L = 70
5). Nilai rata-rata adonan : x_g = 65

Perbandingan jumlah pria dan wanita:

⇒	nL	=	nP
	xL – xg		xg – xP

⇒	nL	=	nP
	70 – 65		65 – 63

⇒ n_L/n_P = 5/2
⇒ n_L : n_P = 5 : 2

Contoh 9: Menentukan Jangkauan Kuartil Data

Diberikan data sebagai berikut: 85, 80, 82, 81, 83, 86, 88
Jangkauan kuartil atau hamparan dari data di atas yaitu …
A. H = 5
B. H = 4
C. H = 3
D. H = 2

Pembahasan :
Untuk memilih jangkauan kuartil, datanya harus kita urutkan terlebih dulu dari terkecil ke terbesar.

Urutan data: 80, 81, 82, 83, 85, 86, 88
Dik : Q₁ = 81, Q₂ = 83, Q₃ = 86

Jangkauan kuartil atau hamparan:
⇒ H = Q₃ – Q₁
⇒ H = 86 – 81
⇒ H = 5

Contoh 10: Menentukan Nilai Kuartil Bawah
Kuartil bawah dari data : 5, 5, 7, 7, 6, 8, 7, 8, 9 ialah …
A. 5,0
B. 5,5
C. 6,0
D. 8,0

Pembahasan :
Kuartil yakni ukuran yang membagi data menjadi 4 bagian yang serupa. Kuartil bawah (Q₁) terletak di sebelah kiri median.

Urutan data : 5, 5, 6, 7, 7, 7, 8, 8, 9
⇒ Q₁ = (5 + 6)/2
⇒ Q₁ = 11/2
⇒ Q₁ = 5,5