Daftar Isi
Matematika kls 8 semester 2 ayo kita berlatih 6.2
Ayo Berlatih 6.2 Kelas 8 semester2, merupakan materi Teorama Pythagoras yg terdapat pada buku paket Matematika revisi 2017 halaman 22 – 24. Saya akan menjawab 5 no soal yg terdapat pada lampiran.
Pembahasan
No 1.
Tentukan jarak antara dua titik dr pasangan berikut
Jawab :
a. (10 , 20) dan (13 , 16)
Jarak a = [tex]\sqrt ( x_ 2 -x_ 1 ) ^ 2 + (y_ 2 – y_ 1 ) ^ 2 [/tex]
= [tex]\sqrt (13 – 10)^ 2 + (16 – 20)^ 2 [/tex]
= [tex]\sqrt 3^ 2 + (-4)^ 2 [/tex]
= [tex]\sqrt 9 + 16 [/tex]
= √25
= 5
b. (15 , 37) dan (42 , 73)
Jarak b = [tex]\sqrt ( x_ 2 -x_ 1 ) ^ 2 + (y_ 2 – y_ 1 ) ^ 2 [/tex]
= [tex]\sqrt (42 – 15)^ 2 + (73 – 37)^ 2 [/tex]
= [tex]\sqrt 27^ 2 + 36^ 2 [/tex]
= [tex]\sqrt 729 + 1296 [/tex]
= √2025
= 45
c. (-19 , -16) dan (-2 , 14)
Jarak c = [tex]\sqrt ( x_ 2 -x_ 1 ) ^ 2 + (y_ 2 – y_ 1 ) ^ 2 [/tex]
= [tex]\sqrt (-2 – (-19))^ 2 + (14 – (-16))^ 2 [/tex]
= [tex]\sqrt (-2 + 19)^ 2 + (14 + 16)^ 2 [/tex]
= [tex]\sqrt 17^ 2 + 30^ 2 [/tex]
= [tex]\sqrt 289 + 900 [/tex]
= √1189
= 34,48
No 2.
Diketahui ∆ ABC dgn titik-titik A (-1 , 5), B (-1 , 1), & C (2 , 1). Apakah segitiga ABC merupakan segitiga siku-siku? Jelaskan.
Jawab :
A (-1 , 5), B (-1 , 1), & C (2 , 1).
Panjang AB = [tex]\sqrt ( x_ 2 -x_ 1 ) ^ 2 + (y_ 2 – y_ 1 ) ^ 2 [/tex]
= [tex]\sqrt ( -1 – (-1)) ^ 2 + (1 – 5) ^ 2 [/tex]
= [tex]\sqrt 0^ 2 + (-4)^ 2 [/tex]
= √16
= 4 satuan
Panjang BC = [tex]\sqrt (2-(-1))^ 2 + (1-1)^ 2 [/tex]
= [tex]\sqrt 3^ 2 + (0)^ 2 [/tex]
= √9
= 3 satuan
Panjang AC = [tex]\sqrt (2 – (-1)) ^ 2 + (1 – 5) ^ 2 [/tex]
= [tex]\sqrt (3)^ 2 + (-4)^ 2 [/tex]
= [tex]\sqrt 9 + 16 [/tex]
= √25
= 5 satuan
Pembuktian
AB² + BC² = AC²
4² + 3² = 5²
16 + 9 = 25
25 = 25
Kaprikornus Δ ABC merupakan segitiga siku-siku, karena ketiga sisinya merupakan tripel pythagoras.
No 3.
Tentukan luas tempat yg diarsir dr setiap gambar berikut
a² + b² = c²
b² = 20² – 16²
b² = 400 – 256
b² = 144
b = √144
b = 12
jari-jari setengah bundar = 12/2 = 6 cm
L arsir 1/2 bundar = 1/2 π r²
= 1/2 × 3,14 × 6 × 6 cm²
= 3,14 × 18 cm²
= 56,52 cm²
L segitiga = 1/2 × a × t
= 1/2 × 16 × 12 cm²
= 96 cm²
Jadi luas yg diarsir setengah bundar yaitu 56,52 cm²
No. b
Δ ABC
AB² = AC² + BC²
AB² = 20² + 15²
AB² = 400 + 225
AB² = 625
AB = √625
AB = 25 cm
L Δ ABC = 1/2 × AC × BC
= 1/2 ×20 × 15 cm²
= 150 cm²
Δ ACD
AC² = AD² + CD²
CD² = 20² – 12²
CD² = 400 – 144
CD² = 256
CD = √256
CD = 16 cm
L Δ ACD = 1/2 × AD × CD
= 1/2 × 12 × 16 cm²
= 96 cm²
L seluruh = L Δ ABC + L Δ ACD
= 150 cm² + 96 cm²
= 246 cm²
Jadi luas diarsir ABCD ialah 246 cm²
No 4.
Guru meminta kalian untuk menentukan jarak antara dua titik (4,2) & (7,6). ananda menggunakan (4,2) selaku (x1,y1) sedangkan temanmu memakai (7,6) selaku (x1,y1). apakah ananda & temanmu memperoleh hasil yg sama? jelaskan
Jawab :
Hasilnya akan sama.
Karena titik koordinat yg diberikan sama, maka jaraknya akan sama
No 5.
Ahmad berlangsung 20 langkah ke depan kemudian 15 langkah ke kanan. Pada saat yg sama, Udin berjalan 16 langkah ke depan kemudian 12 langkah ke kanan. Udin berhenti lalu menembak Ahmad.
- a. Gambar suasana di atas dgn memakai bidang kartesius.
- b. Berapa langkah jarak mereka berdua ketika Udin menembak Ahmad dgn pistol bambu?
Jawab :
a. Gambar suasana dr pernyataan diatas bisa dilihat pada lampiran II
b.
I. Menghitung petak langkah dgn memakai pythagoras
c² = a² + b²
AU² = (20 + 16)² + (15 + 12)
= 36² + 27²
= 1296 + 729
= 2025
AU = √2025
AU = 45 satuan langkah
Jadi jarak mereka berdua ketika Udin menembak Ahmad dgn pistol bambu adalh 45 langkah.
II. Menghitung jarak dua titik antara Ahmad & Udin yaitu (-20 , 15) & (16 , -12)
Jarak AU = [tex]\sqrt (x_ 2 -x_ 1 ) ^ 2 + (y_ 2 – y_ 1 ) ^ 2 [/tex]
= [tex]\sqrt (16 – (-20))^ 2 + (-12 – 15)^ 2 [/tex]
= [tex]\sqrt 36^ 2 + (-27)^ 2 [/tex]
= [tex]\sqrt 1296 + 729 [/tex]
= √2025
= 45 langkah
Makara jarak mereka berdua saat Udin menembak Ahmad dgn pistol bambu adalh 45 langkah.
No.6. wargamasyarakat.org/tugas/13795354
No 9. https://wargamasyarakat.org/peran/13875726
No. 10. wargamasyarakat.org/peran/13822842
Pelajari Lebih lanjut ihwal Teorama Pythagoras
- Diketahui persegi panjang ABCD & P merupakan titik di dlm persegi panjang.Jika PC = 8 cm, PD = 4 cm, & PB = 7 cm, maka PA → wargamasyarakat.org/tugas/13821934
- Bilangan terkecil dr tripel pythagoras ialah 33. jelaskan bagaimana kalian mendapatkan dua bilangan lainnya → https://wargamasyarakat.org/peran/14086821
- Lengkapi tabel berikut menurut ketiga segitiga yg sudah kalian buat → wargamasyarakat.org/tugas/20941905
- Ayo kita berlatih 6.1, Jawaban matematika kelas 8 semester 2 halaman 11 – 13 → wargamasyarakat.org/tugas/20942033
Detil Jawaban
- Kelas : 8 Sekolah Menengah Pertama
- Mapel : Matematika
- Bab : 4 – Teorama Pythagoras
- Kode : 8.2.4
- Kata kunci : Tripel pythagoras, Ayo berlatih 6.2
Semoga bermanfaat

jawaban matematika kelas 8 semester 2 halam 23 ayo berlatih 6.2
Jawaban:
jawaban matematika kelas 8 semester 2 halam 23 ayo berlatih 6.2
6. Seorang atlet tenis mengajukan pertanyaan pada wasit. Suara atlet mampu didengar wasit cuma pada jarak maksimum 30 kaki. Berdasarkan posisi wasit & atlet tenis pada gambar berikut, dapatkah wasit mendengar bunyi sang atlet? Jelaskan tanggapan kalian.
Jawaban:
Jarak = √(24² – (12 – 5)²)
= √(24² + (12 – 5)² )
= √(576 + 49)
= √625
= 25 kaki
Kaprikornus , Anda mampu mendengar bunyi atlet alasannya adalah jarak mereka berdua cuma 25 kaki & jarak dengar maksimum ialah 30 kaki.
7. Tinggi sebuah jendela lantai 2 pada suatu gedung kira-kira 8 meter. Di depan gedung tersebut ada sebuah taman dgn lebar 6 m.
Berapakah panjang tangga minimum yg dibutuhkan biar kaki-kaki tangga tak merusak taman tersebut?
Jawaban:
Panjang Tangga
= √(8² + 6²)
= √(64 + 36)
= √100
= 10 m.
Kaprikornus , panjang tangga minimum agar kaki-kaki tangga tak merusak taman yaitu 10 meter.
Advertisement
8. Seorang penyelam dr Tim SAR mengaitkan dirinya pada tali sepanjang 25 m untuk mencari sisa-sisa bangkai pesawat di dasar bahari. Laut
diselami memiliki kedalaman 20 meter & dasarnya rata. Berapakah luas tempat yang
bisa dijangkau oleh penyelam tersebut?
Jawaban:
Jari-jari = √(25² – 20²)
= √(625 – 400)
= √225
= 15 m
Luas tempat = π xrxr
= 3,14 x 15 x 15
= 706,5 m²
Jadi , luas daerah yg dapat dijangkau oleh penyelam tersebut adalah 706,5 m².
9. Tentukan panjang AG dr bangun berikut.
Jawaban:
a. AE = 10 EG
= √(HG² + GF²)
= √(10² + 10²)
= √(100 + 100)
= √200 AG
= √(AE² + EG²)
= √(10² + √200²)
= √(100 + 200)
= √300
= 10√3
Jadi , panjang AG yakni 10√3.
b. HG = 5 AH
= √(AD² + DH²)
= √(5² + 10² )
= √(25 + 100)
= √125 AB
= √(HG² + AH²)
= √(5² + √125² )
= √(25 + 125)
= √150
= 5√6
Kaprikornus , panjang AG yaitu 5√6.
10. Bola A & bola B digantung pada suatu kawat lurus seperti pada gambar di samping.
Diameter Bola A & Bola B berturut-turut adalah 8 & 18. Jika jarak ujung tali l & n pada kawat yaitu 5 & panjang tali l yaitu 10, berapakah panjang minimum tali n semoga kedua tali bisa sejajar & bola tak saling menekan?
Jawaban:
l = 10 satuan
BC = 9 satuan
AD = FE = 5 satuan
ED = FA = 4 satuan
AB = 4 + 9 = 13 satuan
BD = √(AB² – AD²)
= √(13² – 5²)
= √(169 – 25)
= √144
= 12 satuan
n = l + ED + (BD – BC)
= 10 + 4 + (12 – 9)
= 17 satuan
Makara , panjang minimum tali n ialah 17 satuan.
Ayo Kita Berlatih 6.2 Kelas 7 semester 2
Ayo Kita Berlatih 6.2 Kelas 7 semester 2 Halaman 83 (Aritmatika Sosial)
Saya akan membahas no 1 – 5
Rumus :
Bunga = [tex]\frac suku\:bunga 100 [/tex] x Pinjaman permulaan
Pembahasan :
1. Pak Adi meminjam uang di bank sebesar Rp 30.000.000 dgn bunga 24% pertahun. Tentukan bunga yg ditanggung oleh Pak Adi jika akan meminjam selama :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Diketahui :
Pinjaman awal = Rp 30.000.000
Bunga = 24% / tahun
Ditanya :
Bunga yg ditanggung untuk :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Dijawab :
a. Bunga untuk 6 bulan = [tex]\frac 6 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 3.600.000
b. Bunga untuk 8 bulan = [tex]\frac 8 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 4.800.000
c. Bunga untuk 12 bulan = [tex]\frac 12 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 7.200.000
d. Bunga untuk 16 bulan = [tex]\frac 16 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 9.600.000
e. Bunga untuk 18 bulan = [tex]\frac 18 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 10.800.000
f. Bunga untuk 24 bulan = [tex]\frac 24 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 14.400.000
2. Pak Budi meminjam duit di Bank sebesar Rp 30.000.000 dgn bunga 24% pertahun. Tentukan keseluruhan nominal yg mesti dikembalikan Pak Budi bila akan meminjam selama :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Diketahui :
Pinjaman permulaan = Rp 30.000.000
Bunga = 24% / tahun
Ditanya :
Keseluruhan yg mesti dikembalikan untuk jangka waktu :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Dijawab :
a. Bunga untuk 6 bulan = [tex]\frac 6 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 3.600.000
Nominal yg harus dibayar untuk 6 bulan = Rp 30.000.000 + Rp 3.600.000 = Rp 33.600.000
b. Bunga untuk 8 bulan = [tex]\frac 8 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 4.800.000
Nominal yg mesti dibayar untuk 8 bulan = Rp 30.000.000 + Rp 4.800.000 = Rp 34.800.000
c. Bunga untuk 12 bulan = [tex]\frac 12 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 7.200.000
Nominal yg mesti dibayar untuk 12 bulan = Rp 30.000.000 + Rp 7.200.000 = Rp 37.200.000
d. Bunga untuk 16 bulan = [tex]\frac 16 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 9.600.000
Nominal yg mesti dibayar untuk 16 bulan = Rp 30.000.000 + Rp 9.600.000 = Rp 39.600.000
e. Bunga untuk 18 bulan = [tex]\frac 18 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 10.800.000
Nominal yg mesti dibayar untuk 18 bulan = Rp 30.000.000 + Rp 10.800.000 = Rp 40.800.000
f. Bunga untuk 24 bulan = [tex]\frac 24 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 14.400.000
Nominal yg mesti dibayar untuk 24 bulan = Rp 30.000.000 + Rp 14.400.000 = Rp 44.400.000
3. Pak yudi akan meminjam uang di bank dgn persentase bunga sebesar 10% pertahun. Besar duit yg dipinjam oleh Pak Yudi adalah 12 juta rupiah. Jika Pak Yudi berniat meminjam duit selama 1 tahun, pastikan :
a. Besar keseluruhan bunga yg mesti ditanggung oleh Pak Yudi?
b. Besar angsuran yg harus dibayarkan, kalau Pak Yudi mesti mengangsur tiap bulan dgn nominal yg sama?
Diketahui :
Pinjaman permulaan = Rp 12.000.000
Bunga = 10% / tahun
Ditanya :
a. Bunga selama 1 tahun ?
b. Angsuran yg harus dibayar selama 1 tahun ?
Dijawab :
a. Bunga 1 tahun = [tex]\frac 10 100 [/tex] x Rp 12.000.000 = Rp 1.200.000
b. Pokok + bunga setahun = Rp 12.000.000 + Rp 1.200.000 = Rp 13.200.000
Angsuran yg mesti dibayar tiap bulan = Rp 13.200.000 : 12 = Rp 1.100.000
4. Pak Agus meminjam duit di Bank sebesar Rp 20.000.000. Dalam 1 tahun besar yg mesti diangsur ialah Rp 23.600.000 Tentukan :
a. Besar bunga yg ditanggu Pak Agus selama setahun?
b. Besar bunga yg ditanggung Pak Agus tiap bulan ?
c. Besar persentase bunga pertahun yg ditanggung Pak Agus?
d. Besar persentase bunga perbulan yg ditanggung Pak Agus?
Diketahui :
Pinjaman awal = Rp 20.000.000
Pinjaman + bunga setahun = Rp 23.600.000
Ditanya :
a. Bunga selama setahun?
b. Bunga selama sebulan?
c. Persentase bunga setahun ?
d. Persentase bunga sebulan?
Dijawab :
a. Bunga selama setahun = Rp 23.600.000 – Rp 20.000.000 = Rp 3.600.000
b. Bunga selama sebulan = Rp 3.600.000 : 12 = Rp 300.000
c. Persentase bunga setahun = [tex]\frac 3.600.000 20.000.000 [/tex] x 100% = 18%
d. Persentase bunga sebulan = [tex]\frac 300.000 20.000.000 [/tex] x 100% = 1,5%
Pelajari lebih lanjut :
Soal-soal perihal Aritmatika sosial :
1. https://wargamasyarakat.org/peran/21335926
2. https://wargamasyarakat.org/peran/21318766
3. https://wargamasyarakat.org/peran/21275837
========================
Detail Jawaban :
Kelas : VII
Mapel : Matematika
Bab : Bab 7 – Aritmatika Sosial
Kode : 7.2.7
Kata Kunci : ayo kita berlatih 6.2, kelas 7 semester 2, halaman 83, bunga, dukungan

Apa tanggapan ayo kita berlatih 6.2 kls 7 semester 2 matematika
Jawaban ayo kita berlatih 6.2 kls 7 semester 2 matematika
Pada soal-soal ini kita akan membahas perihal bunga pertolongan (Aritmatika sosial)
Saya akan membahas no 1 – 5
Rumus :
Bunga = [tex]\frac suku\:bunga 100 [/tex] x Pinjaman permulaan
Pembahasan :
1. Pak Adi meminjam duit di bank sebesar Rp 30.000.000 dgn bunga 24% pertahun. Tentukan bunga yg ditanggung oleh Pak Adi kalau akan meminjam selama :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Diketahui :
Pinjaman awal = Rp 30.000.000
Bunga = 24% / tahun
Ditanya :
Bunga yg ditanggung untuk :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Dijawab :
a. Bunga untuk 6 bulan = [tex]\frac 6 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 3.600.000
b. Bunga untuk 8 bulan = [tex]\frac 8 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 4.800.000
c. Bunga untuk 12 bulan = [tex]\frac 12 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 7.200.000
d. Bunga untuk 16 bulan = [tex]\frac 16 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 9.600.000
e. Bunga untuk 18 bulan = [tex]\frac 18 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 10.800.000
f. Bunga untuk 24 bulan = [tex]\frac 24 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 14.400.000
2. Pak Budi meminjam uang di Bank sebesar Rp 30.000.000 dgn bunga 24% pertahun. Tentukan keseluruhan nominal yg harus dikembalikan Pak Budi bila akan meminjam selama :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Diketahui :
Pinjaman awal = Rp 30.000.000
Bunga = 24% / tahun
Ditanya :
Keseluruhan yg harus dikembalikan untuk jangka waktu :
a. 6 bulan d. 16 bulan
b 8 bulan e. 18 bulan
c. 12 bulan f. 24 bulan
Dijawab :
a. Bunga untuk 6 bulan = [tex]\frac 6 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 3.600.000
Nominal yg harus dibayar untuk 6 bulan = Rp 30.000.000 + Rp 3.600.000 = Rp 33.600.000
b. Bunga untuk 8 bulan = [tex]\frac 8 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 4.800.000
Nominal yg harus dibayar untuk 8 bulan = Rp 30.000.000 + Rp 4.800.000 = Rp 34.800.000
c. Bunga untuk 12 bulan = [tex]\frac 12 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 7.200.000
Nominal yg harus dibayar untuk 12 bulan = Rp 30.000.000 + Rp 7.200.000 = Rp 37.200.000
d. Bunga untuk 16 bulan = [tex]\frac 16 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 9.600.000
Nominal yg harus dibayar untuk 16 bulan = Rp 30.000.000 + Rp 9.600.000 = Rp 39.600.000
e. Bunga untuk 18 bulan = [tex]\frac 18 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 10.800.000
Nominal yg mesti dibayar untuk 18 bulan = Rp 30.000.000 + Rp 10.800.000 = Rp 40.800.000
f. Bunga untuk 24 bulan = [tex]\frac 24 12 \times \frac 24 100 [/tex] x Rp 30.000.000 = Rp 14.400.000
Nominal yg harus dibayar untuk 24 bulan = Rp 30.000.000 + Rp 14.400.000 = Rp 44.400.000
3. Pak yudi akan meminjam uang di bank dgn persentase bunga sebesar 10% pertahun. Besar uang yg dipinjam oleh Pak Yudi yaitu 12 juta rupiah. Jika Pak Yudi bermaksud meminjam duit selama 1 tahun, pastikan :
a. Besar keseluruhan bunga yg mesti ditanggung oleh Pak Yudi?
b. Besar angsuran yg mesti dibayarkan, kalau Pak Yudi harus mengangsur tiap bulan dgn nominal yg sama?
Diketahui :
Pinjaman permulaan = Rp 12.000.000
Bunga = 10% / tahun
Ditanya :
a. Bunga selama 1 tahun ?
b. Angsuran yg harus dibayar selama 1 tahun ?
Dijawab :
a. Bunga 1 tahun = [tex]\frac 10 100 [/tex] x Rp 12.000.000 = Rp 1.200.000
b. Pokok + bunga setahun = Rp 12.000.000 + Rp 1.200.000 = Rp 13.200.000
Angsuran yg mesti dibayar tiap bulan = Rp 13.200.000 : 12 = Rp 1.100.000
4. Pak Agus meminjam duit di Bank sebesar Rp 20.000.000. Dalam 1 tahun besar yg harus diangsur yakni Rp 23.600.000 Tentukan :
a. Besar bunga yg ditanggu Pak Agus selama setahun?
b. Besar bunga yg ditanggung Pak Agus tiap bulan ?
c. Besar persentase bunga pertahun yg ditanggung Pak Agus?
d. Besar persentase bunga perbulan yg ditanggung Pak Agus
Diketahui :
Pinjaman awal = Rp 20.000.000
Pinjaman + bunga setahun = Rp 23.600.000
Ditanya :
a. Bunga selama setahun?
b. Bunga selama sebulan?
c. Persentase bunga setahun ?
d. Persentase bunga sebulan?
Dijawab :
a. Bunga selama setahun = Rp 23.600.000 – Rp 20.000.000 = Rp 3.600.000
b. Bunga selama sebulan = Rp 3.600.000 : 12 = Rp 300.000
c. Persentase bunga setahun = [tex]\frac 3.600.000 20.000.000 [/tex] x 100% = 18%
d. Persentase bunga sebulan = [tex]\frac 300.000 20.000.000 [/tex] x 100% = 1,5%
Pelajari lebih lanjut :
Soal-soal wacana Aritmatika sosial :
1. wargamasyarakat.org/tugas/21335926
2. wargamasyarakat.org/peran/21318766
3. wargamasyarakat.org/tugas/21275837
========================
Detail Jawaban :
Kelas : VII
Mapel : Matematika
Bab : Bab 7 – Aritmatika Sosial
Kode : 7.2.7
Kata Kunci : ayo kita berlatih 6.2, kelas 7 semester 2, halaman 83, bunga, pinjaman

Kunci balasan matematika kelas 7 semester 2 ayo kita berlatih 6.2 nomor 15 ,16,17,18
Kunci tanggapan matematika kelas 7 semester 2 ayo kita berlatih 6.2 nomor 15 ,16,17,18
Pada soal ini kita membicarakan perihal bunga, discount, untung, rugi ataupun impas
Suatu keadaan dikatakan untung apabila harga jual lebih besar daripada harga beli
Suatu keadaan dibilang rugi apabila harga jual lebih rendah ketimbang harga beli
Suatu kondisi dibilang impas apabila harga jual sama dgn harga beli
Pembahasan :
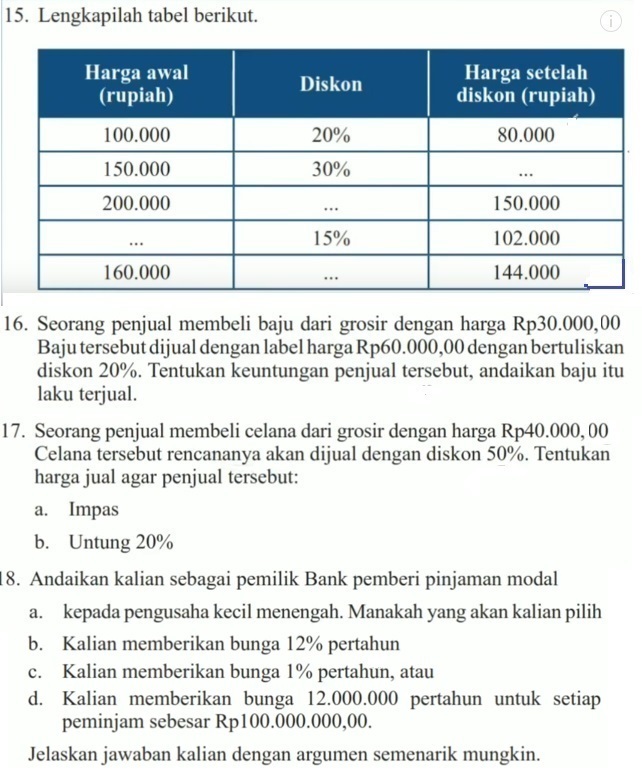
15. Lengkapi tabel berikut :
Harga permulaan Diskon Harga setelah
(Rupiah) Diskon (Rupiah)
100.000 20% 80.000
150.000 30% ….
200.000 …. 150.000
…. 15% 102.000
160.000 …. 144.000
Diketahui :
Harga permulaan Rp 150.000
Diskon 30%
Ditanya :
Harga sehabis potongan harga ?
Diskon = [tex]\frac 30 100 [/tex] x Rp 150.000 = Rp 45.000
Harga setelah potongan harga = Rp 150.000 – Rp 45.000 = Rp 105.000
Diketahui :
Harga permulaan Rp 200.000
Harga sehabis diskon Rp 150.000
Ditanya :
DIskon ?
Dijawab :
Diskon = Rp 200.000 – Rp 150.000 = Rp 50.000
Persentase potongan harga = [tex]\frac 50.000 200.000 [/tex] x 100% = 25%
Diketahui :
Diskon 15%
Harga sehabis diskon Rp 102.000
Ditanya :
Harga awal ?
Dijawab :
Harga setelah diskon = Harga awal – ([tex]\frac 100 15 [/tex] x Harga permulaan)
102.000 = Harga awal – ([tex]\frac 100 15 [/tex] x Harga permulaan)
102.000 = Harga awal – (0,15 Harga awal)
102.000 = 0,85 Harga awal
Harga permulaan = 102.000 : 0,85
Harga permulaan = 120.000
Diketahui :
Harga permulaan Rp 160.000
Harga sehabis diskon Rp 144.000
Ditanya :
Diskon ?
Dijawab :
Diskon = Rp 160.000 – Rp 144.000 = Rp 16.000
Persentase diskon = [tex]\frac 16.000 160.000 [/tex] x 100% = 10%
16. Seorang penjual berbelanja baju dr grosir dgn harga Rp 30.000. Baju tersebut dijual dgn label harga Rp 60.000 dgn bertuliskan diskon 20%. Tentukan laba pedagang tersebut, andaikan baju itu laris terjual.
Diketahui :
Harga beli Rp 30.000
Harga jual Rp 60.000
Diskon penjualan 20%
Ditanya :
Keuntungan pedagang tersebut?
Dijawab :
Kita cari dulu harga jual baju tersebut
Diskon = [tex]\frac 20 100 [/tex] x Rp 60.000 = Rp 12.000
Harga jual = Rp 60.000 – Rp 12.000 = Rp 48.000
Keuntungan pedagang = Rp 48.000 – Rp 30.000 = Rp 18.000
Persentase keuntungan = [tex]\frac 18.000 30.000 [/tex] x 100% = 60%
17. Seorang penjual membeli celana dr grosir dgn harga Rp 40.000. Celana tersebut rencananya akan dijual dgn potongan harga 50%. Tentukan harga jual supaya penjual tersebut :
a. Impas
b. Untung 20%
Diketahui :
Harga beli Rp 40.000
Diskon pemasaran 50%
Ditanya :
Harga jual agar :
a. Impas
b. Untung 20%
Ditanya :
a. Agar terjadi impas maka harga beli = harga jual
Harga jual sesudah diskon = Rp 40.000
Diskon = 50%
Harga jual sesudah potongan harga = Harga jual – (50% x Harga jual)
40.000 = Harga jual – 0,5 Harga jual
40.000 = 0,5 Harga jual
Harga jual = 40.000 : 0,5
Harga jual = Rp 80.000
b. Agar terjadi untung 20%
Harga beli Rp 40.000
Untung = [tex]\frac 20 100 [/tex] x Rp 40.000 = Rp 8.000
Harga jual sehabis diskon = Rp 40.000 + Rp 8.000 = Rp 48.000
Harga jual sesudah diskon = Harga jual – (50% x Harga jual)
48.000 = Harga jual – 0,5 Harga jual
48.000 = 0,5 Harga jual
Harga jual = 48.000 : 0,5
Harga jual = Rp 96.000
18. Andaikan kalian sebagai pemilik bank pemberi dukungan modal
a. Pada pengusaha kecil menangah. Manakah yg akan kalian pilih
b. Kalian memberikan bunga 12% pertahun
c. Kalian memberikan bunga 1% pertahun
d. Kalian menunjukkan bunga Rp 12.000 pertahun untuk setiap perlindungan sebesar Rp 100.000.000
Jelaskan jawaban kalian dgn argumen sebagus mungkin
Diketahui :
Saya sebagai pemilik modal maka pilihan yg paling menarik yaitu :
b. Kalian menunjukkan bunga 12% pertahun
c. Kalian memperlihatkan bunga 1% pertahun
d. Kalian menunjukkan bunga Rp 12.000 pertahun untuk setiap derma sebesar Rp 100.000.000
Ditanya :
Jelaskan pilihan yg akan kalian tentukan ?
Dijawab :
yang potongan a masih merupakan soal, maka tak saya jelaskan
b. Kalian memberikan bunga 12% pertahun
Bunga 12% setahun merupakan bunga yg cukup besar, nanti kita akan bandingkan dgn pilihan yang lain
c. Kalian memperlihatkan bunga 1% pertahun
Bunga 1% masih lebih kecil ketimbang bunga 12% pertahun, jadi pilihan yg b masih lebih baik daripada ini.
Karena bunga 1% akan lebih kecil ketimbang 12%
d. Kalian menawarkan bunga Rp 12.000 pertahun untuk setiap perlindungan sebesar Rp 100.000.000
Pertama-tama kita hitung dahulu persentase bunganya
Persentase bunga = [tex]\frac 12.000 100.000.000 [/tex] x 100% = 0,012%
Jelas ini suku bunga terkecil dibandingkan pilihan b & c
∴ Maka saya sebagai pemilik modal akan memberikan opsi b, yaitu bunga 12% pertahun, sebab itu merupakan bunga terbesar dibanding pilihan lainnya
Pelajari lebih lanjut :
Soal-soal wacana Aritmatika sosial :
1. https://wargamasyarakat.org/peran/21607711
2. https://wargamasyarakat.org/peran/21591840
====================
Detail Jawaban :
Kelas : VII
Mapel : Matematika
Bab : Bab 7 – Aritmatika sosial
Kode : 7.2.7
Kata Kunci : ayo kita berlatih 6.2, kelas 7 semester 2, potongan harga, harga modal, harga jual